题目内容
设ω＞0，若函数f（x）=2sinωx在[-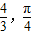
]上单调递增，则ω的取值范围是______．
【答案】分析：依题意，f（x）=2sinωx在[-
，
]上单调递增，从而可求得ω的取值范围．
解答：解：∵ω＞0，若函数f（x）=2sinωx在[-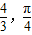
]上单调递增，
∴f（x）=2sinωx在[-
，
]上单调递增，
∴
T=
•
≥
，
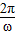∴0＜ω≤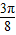
．
故答案为：（0，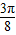
]．
点评：本题考查正弦函数的单调性，考查分析运算能力，属于中档题．
，]上单调递增，从而可求得ω的取值范围．解答：解：∵ω＞0，若函数f（x）=2sinωx在[-
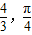]上单调递增，∴f（x）=2sinωx在[-
，]上单调递增，∴
T=•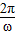≥，∴0＜ω≤
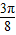．故答案为：（0，
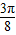]．点评：本题考查正弦函数的单调性，考查分析运算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目