题目内容
某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的,若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金,若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其它区域则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则能与了促销活动.(Ⅰ) 求顾客甲中一等奖的概率;
(Ⅱ) 记ξ为顾客甲所得的奖金数,求ξ的分布列及其数学期望.

【答案】分析:(Ⅰ) 设事件A表示该顾客中一等奖,利用排列组合知识能求出该顾客中一等奖的概率.
(Ⅱ)ξ的可能取值为20,15,10,5,0,分别求出P(ξ=20),P(ξ=15),P(ξ=10),P(ξ=5),P(ξ=0),由此能求出ξ的分布列和数学期望Eξ.
解答:解:(Ⅰ) 设事件A表示该顾客中一等奖,
则P(A)= ×
× =
= .
.
所以该顾客中一等奖的概率是 .
.
(Ⅱ)ξ的可能取值为20,15,10,5,0
P(ξ=20)= =
= ,P(ξ=15)=2×
,P(ξ=15)=2× =
= ,
,
P(ξ=10)= =
= ,
,
P(ξ=5)=2× ×
× =
= ,P(ξ=0)=
,P(ξ=0)= =
= ,(每个1分)
,(每个1分)
所以ξ的分布列为
数学期望Eξ=20× +15×
+15× +10×
+10× +5×
+5× =
= .
.
点评:本题考查离散型随机变量的分布列和数学期望,解题时要认真审题,注意排列组合知识的合理运用.
(Ⅱ)ξ的可能取值为20,15,10,5,0,分别求出P(ξ=20),P(ξ=15),P(ξ=10),P(ξ=5),P(ξ=0),由此能求出ξ的分布列和数学期望Eξ.
解答:解:(Ⅰ) 设事件A表示该顾客中一等奖,
则P(A)=
 ×
× =
= .
.所以该顾客中一等奖的概率是
 .
.(Ⅱ)ξ的可能取值为20,15,10,5,0
P(ξ=20)=
 =
= ,P(ξ=15)=2×
,P(ξ=15)=2× =
= ,
,P(ξ=10)=
 =
= ,
,P(ξ=5)=2×
 ×
× =
= ,P(ξ=0)=
,P(ξ=0)= =
= ,(每个1分)
,(每个1分)所以ξ的分布列为
| ξ | 20 | 15 | 10 | 5 | |
| P |  |  |  |  |  |
 +15×
+15× +10×
+10× +5×
+5× =
= .
.点评:本题考查离散型随机变量的分布列和数学期望,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
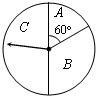 某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.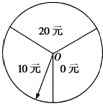 某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等.假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满100元可以转动如图所示的圆盘一次,其中O为圆心,且标有20元、10元、0元的三部分区域面积相等.假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例如:某顾客消费了218元,第一次转动获得了20元,第二次获得了10元,则其共获得了30元优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
 某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的,若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金,若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其它区域则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则能与了促销活动.
某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的,若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金,若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其它区域则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则能与了促销活动.