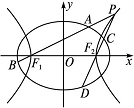
题目内容
若双曲线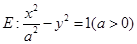 的离心率等于
的离心率等于 ,直线
,直线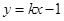 与双曲线
与双曲线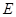 的右支交于
的右支交于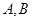 两点.
两点.
(1)求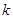 的取值范围;
的取值范围;
(2)若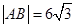 ,点
,点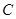 是双曲线
是双曲线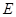 上一点,且
上一点,且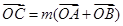 ,求
,求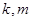
(1) (2)
(2) ,
,
解析试题分析:(1)由 得
得
故双曲线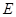 的方程为
的方程为 2分
2分
设 ,
,
由 得
得 4分
4分
又直线与双曲线右支交于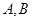 两点,所以
两点,所以 解得
解得 -----6分
-----6分
(2) 


得 
∴ 或
或 又
又 ∴
∴ 9分
9分
那么 ,
,
设 ,由已知
,由已知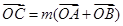 ,得
,得
∴
∴ ,得
,得
故 ,
, .----------14分
.----------14分
考点:双曲线方程及性质,直线与双曲线的位置关系
点评:直线与双曲线相交时常联立方程组,转化为关于x或y的二次方程,利用韦达定理设而不求的方法
再将所求问题用根与系数的关系的表示

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
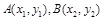 是椭圆
是椭圆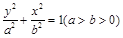 上的两点,已知向量
上的两点,已知向量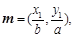
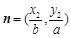 ,若
,若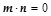 且椭圆的离心率
且椭圆的离心率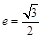 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.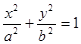
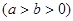 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点 的最短距离为
的最短距离为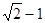 .
.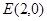 且斜率为
且斜率为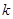 (
( 与C交于
与C交于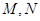 两点,
两点, 是点
是点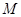 关于
关于 轴的对称点,证明:
轴的对称点,证明: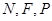 三点共线.
三点共线.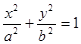 (a>b>0),则称以原点为圆心,r=
(a>b>0),则称以原点为圆心,r=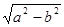 的圆为椭圆C的“知己圆”。
的圆为椭圆C的“知己圆”。 ;求椭圆C方程及其“知己圆”的方程;
;求椭圆C方程及其“知己圆”的方程;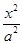 +
+ =1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d.
=1(a>b>0)的上顶点B和左焦点F,直线l被圆x2+y2=4截得的弦长为d. ,求k的值;
,求k的值; ,求椭圆离心率e的取值范围.
,求椭圆离心率e的取值范围.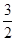 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。 ,
, ,动点
,动点 满足
满足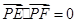 ,由点
,由点 轴作垂线段
轴作垂线段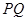 ,垂足为
,垂足为 ,点
,点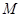 满足
满足 ,点
,点 .
. 作直线
作直线 与曲线
与曲线 ,
, 两点,点
两点,点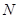 满足
满足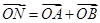 (
( 为原点),求四边形
为原点),求四边形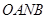 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线 :
: 与双曲线
与双曲线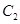 :
: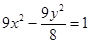 有相同的焦点
有相同的焦点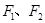 ,
, 是椭圆
是椭圆 的周长为
的周长为 ,求椭圆
,求椭圆 ”的方程为
”的方程为 .设“盾圆
.设“盾圆 的距离为
的距离为 ,
, 的距离为
的距离为 ,求证:
,求证: 为定值;
为定值;
 :
: (
(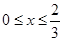 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧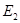 :
: )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆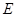 ”.设过点
”.设过点 两点,
两点, ,
,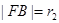 且
且 (
( ),试用
),试用 表示
表示 ;并求
;并求 的取值范围.
的取值范围.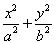 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为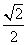 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(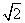 +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.