题目内容
已知函数①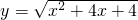
；②y=x2-4x+1（x≤0）；③y=lgx；④
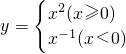那么是从定义域到值域的一一映射的有
- A.①②③
- B.①③④
- C.②③④
- D.①②④
C
分析：若函数f（x）是一一映射，则?x1≠x2，都有f（x1）≠f（x2）．所以一般在定义域内为单调函数的即为一一映射．
解答：①对称轴为x=-2，在（-∞，2）递减，（2，+∞）递增，所以不是一一映射．
②y=x2-4x+1对称轴为x=2，开口向上，所以在（-∞，0）上递减，所以是一一映射．
③在定义域内单调递增，所以是一一映射．
④在[0，+∞）上递增，在（-∞，0）上递减其图象如下图，所以是一一映射．
故选C．
点评：若函数f（x）是一一映射，则?x1≠x2，都有f（x1）≠f（x2）．
所以要判断函数是否为一一映射一般要从两个角度考查：1、单调性 2、图象
分析：若函数f（x）是一一映射，则?x1≠x2，都有f（x1）≠f（x2）．所以一般在定义域内为单调函数的即为一一映射．
解答：①对称轴为x=-2，在（-∞，2）递减，（2，+∞）递增，所以不是一一映射．
②y=x2-4x+1对称轴为x=2，开口向上，所以在（-∞，0）上递减，所以是一一映射．
③在定义域内单调递增，所以是一一映射．
④在[0，+∞）上递增，在（-∞，0）上递减其图象如下图，所以是一一映射．
故选C．
点评：若函数f（x）是一一映射，则?x1≠x2，都有f（x1）≠f（x2）．
所以要判断函数是否为一一映射一般要从两个角度考查：1、单调性 2、图象
练习册系列答案
相关题目
如图，已知椭圆C：
（2013•汕头一模）已知函数．f（x）=Asin（
，
关于y=x对称的图象是
所对应的函数是