题目内容
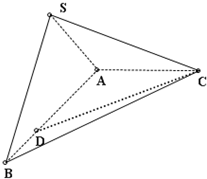
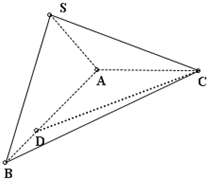
如图所示,在三棱锥S—ABC中,侧棱SA、SB、SC两两垂直,若SO⊥底面ABC于点O,若将此三棱锥沿侧棱展成平面图形恰好可以形成一个边长为a的正方形.

(1)求证:O是底面△ABC的垂心;
(2)求二面角SABC的大小.
答案:解:(1)连结AO、BO,因为侧棱SA、SB、SC两两垂直,易证SA⊥平面SBC、SB⊥平面SAC、SC⊥平面SAB.
所以SA⊥BC,由三垂线定理的逆定理,AO⊥BC,同理可证BO⊥AC.所以O为高线的交点,即为△ABC的垂心.
(2)在三棱锥S—ABC中,过S作SD垂直AB于D,连结CD.因为SC⊥平面SAB,根据三垂线定理,CD⊥AB,所以∠SDC即为所求二面角SABC的平面角.
(注:连结CO并延长交AB于D,连结SD.由CS⊥平面SAB或由SO⊥平面CAB得SD⊥AB.得∠SDC为所求二面角的平面角.)
由于三棱锥的展开图是边长为a的正方形,则B、C分别是SS′和SS″的中点,即SB=SC=![]() ,
,
所以SA=a,AB=![]()
在△SAB中,∠ASB=90°,SB=![]() ,SA=a,AB=
,SA=a,AB=![]() ,所以SD=
,所以SD=![]() .
.
所以tan∠SDC= ,即二面角SABC的大小为arctan
,即二面角SABC的大小为arctan![]() .
.

练习册系列答案
相关题目
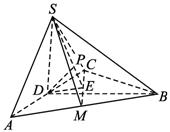
 如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1
如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1(1)求异面直线AB与SC所成的角的余弦值;
(2)在线段AB上求一点D,使CD与平面SAC成45°角.
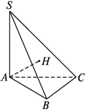
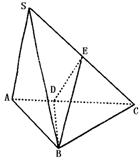 如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.