题目内容
 如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.
解:因为CP∥OB,所以∠CPO=∠POB=60°-θ,∴∠OCP=120°.
在△POC中,由正弦定理得
 =
= ,∴
,∴ =
= ,所以CP=
,所以CP= sinθ.
sinθ.
又 =
= ,∴OC=
,∴OC= sin(60°-θ).
sin(60°-θ).
因此△POC的面积为
S(θ)= CP•OCsin120°=
CP•OCsin120°= •
• sinθ•
sinθ• sin(60°-θ)×
sin(60°-θ)×
= sinθsin(60°-θ)=
sinθsin(60°-θ)= sinθ(
sinθ( cosθ-
cosθ- sinθ)
sinθ)
= (
( sinθcosθ-
sinθcosθ- sin2θ)
sin2θ)
= (
( sin2θ+
sin2θ+ cos2θ-
cos2θ- )
)
= [cos(2θ-60°)-
[cos(2θ-60°)- ],θ∈(0°,60°).
],θ∈(0°,60°).
所以当θ=30°时,S(θ)取得最大值为 .
.
分析:根据CP∥OB求得∠CPO和和∠OCP进而在△POC中利用正弦定理求得PC和OC,进而利用三角形面积公式表示出S(θ)利用两角和公式化简整理后,利用θ的范围确定三角形面积的最大值.
点评:本题主要考查了三角函数的模型的应用.考查了考生分析问题和解决问题的能力.
在△POC中,由正弦定理得
 =
= ,∴
,∴ =
= ,所以CP=
,所以CP= sinθ.
sinθ.又
 =
= ,∴OC=
,∴OC= sin(60°-θ).
sin(60°-θ).因此△POC的面积为
S(θ)=
 CP•OCsin120°=
CP•OCsin120°= •
• sinθ•
sinθ• sin(60°-θ)×
sin(60°-θ)×
=
 sinθsin(60°-θ)=
sinθsin(60°-θ)= sinθ(
sinθ( cosθ-
cosθ- sinθ)
sinθ)=
 (
( sinθcosθ-
sinθcosθ- sin2θ)
sin2θ)=
 (
( sin2θ+
sin2θ+ cos2θ-
cos2θ- )
)=
 [cos(2θ-60°)-
[cos(2θ-60°)- ],θ∈(0°,60°).
],θ∈(0°,60°).所以当θ=30°时,S(θ)取得最大值为
 .
.分析:根据CP∥OB求得∠CPO和和∠OCP进而在△POC中利用正弦定理求得PC和OC,进而利用三角形面积公式表示出S(θ)利用两角和公式化简整理后,利用θ的范围确定三角形面积的最大值.
点评:本题主要考查了三角函数的模型的应用.考查了考生分析问题和解决问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
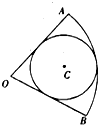 如图圆C内切于扇形AOB,∠AOB=
如图圆C内切于扇形AOB,∠AOB=| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
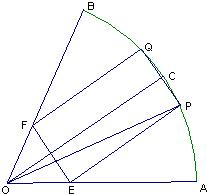 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为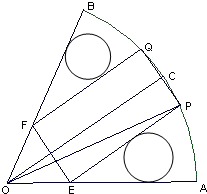 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为 (2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在
(2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在
 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.