题目内容
如图,四棱锥 中,
中, 为矩形,平面
为矩形,平面 平面
平面 .
.

(Ⅰ)求证:
(Ⅱ)若 ,问当
,问当 为何值时,四棱锥
为何值时,四棱锥 的体积最大?并求其最大体积.
的体积最大?并求其最大体积.
(1)证明见解析;(2) ,
, .
.
【解析】
试题分析:(1)利用面面垂直的性质定理进行证明;(2)作辅助线,利用线面垂直找其高线,进而得到关于体积的表达式,利用二次函数的最值求体积的最大值.
试题解析:(1)因为面 面
面 ,面
,面 面
面 =
= ,
,
 面
面 4分
4分
又 面
面 5分
5分
 6分
6分
(2)取 中点,连结
中点,连结 ,
,

 ,由(1)有
,由(1)有 面ABCD, 8分
面ABCD, 8分
设AD= .
.


 当
当 即
即 时,
时,
 .
.
考点:1.空间中垂直关系的转化;2.几何体的体积;3。函数的最值.
考点分析: 考点1:点、线、面之间的位置关系 考点2:柱、锥、台、球的表面积和体积 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取
个小球,分别印有“兰州马拉松”和“绿色金城行”两种标志,摇匀后,规定参加者每次从盒中同时抽取两个小球(登记后放回并摇匀),若抽到的两个小球都印有“兰州马拉松”即可中奖,并停止抽奖,否则继续,但每位嘉宾最多抽取 次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为
次.已知从盒中抽取两个小球不都是“绿色金城行”标志的概率为 .
. 表示某位嘉宾抽奖的次数,求
表示某位嘉宾抽奖的次数,求 的四个命题:
的四个命题: :
: ,
, 

 的共轭复数为
的共轭复数为
 的虚部为
的虚部为
 B.
B. C.
C. D.
D.
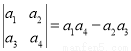 .若将函数
.若将函数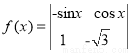 的图象向左平移
的图象向左平移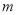
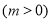 个单位后,所得图象对应的函数为奇函数,则
个单位后,所得图象对应的函数为奇函数,则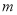 的最小值是( )
的最小值是( )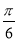 B.
B.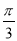 C.
C. D.
D.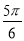
 的四个命题:
的四个命题: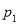 :
: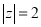 ,
, 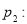
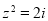
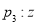 的共轭复数为
的共轭复数为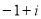
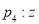 的虚部为
的虚部为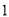
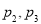 B.
B.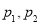 C.
C.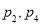 D.
D.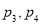

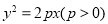 焦点为F,O为坐标原点,M为抛物线上一点,且
焦点为F,O为坐标原点,M为抛物线上一点,且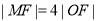 ,
,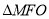 的面积为
的面积为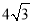 ,则抛物线方程为
,则抛物线方程为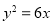 B.
B.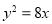 C.
C.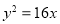 D.
D.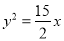
 和等比数列
和等比数列 首项都是1,公差和公比都是2,则
首项都是1,公差和公比都是2,则 .
.