Question

【题目】设是定义在上的函数，对任意实数，，都有，且当时，．

（1）证明:①；②当时，；③是上的增函数；

（2）设，试解关于的不等式．

Answer 1

【答案】（1）证明见解析；（2）当时，，当时，，当时，.

【解析】

试题分析：（1）①利用赋值法，令，解得.②当时，，由已知得，利用，化简得.③任取，由（1）（2）及已知条件知时，，且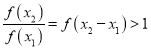，所以函数为增函数；（2）先化简，

即，即，对分类讨论解集的情况.

试题解析：

（1）证明：（1）在中，令，

得即，∴或1，

若，则当时，有与题设矛盾，

∴；

（2）当时，，由已知得，

又，∴，

即时，；

（3）任取，由（1）（2）及已知条件知时，，

则，∵，∴，又因为，

∴，

∴在定义域上为增函数；

（2），

又，在上单调递增，

∴原不等式等价于，

不等式可化为，

∴当，即时，；

当，即时，；

当，即时，．