Question

已知A={x|x²-2x+a≤0},B={x|x²-3x+2≤0},且AB,求实数a的取值范围.

Answer 1

思路分析:欲求实数a的取值范围,只需找出关于a的不等式,据已知条件,易得.

解:得B={x|1≤x≤2},对于A,分以下三种情况:

(1)Δ＜0a＞1,此时A=,满足AB;

4(2)Δ=0a=1,此时A={1},满足AB;

(3)Δ＞0a＜1,此时A={x|1-},要满足AB,

只需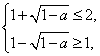且两者等号不同时成立,解得a无解.

综上,可得a的取值范围是［1,+∞).