题目内容
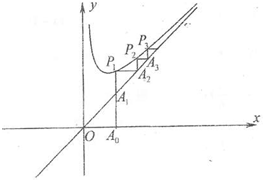 函数f(x)=x+
函数f(x)=x+| 1 | x |
(1)求S1,S2;
(2)求证:yn2=2Tn+2n+x02;
(3)若x0=5,求证:45<y1000<45.1.
分析:(1)显然△A1P1A2为等腰直角三角形,从而有S1=
=
=
,S2=
=
=
=
(2)由图可知An(yn-1,yn-1),,进而可得Sn=
=
=
=
由
=
+
+2得
-
=
+2,
-
=
+2,从而可证yn2=2Tn+2n+x02;
(3)由(2)
=2
+2×1000+25>2025>452,
=2
+2×100+25>225
=2
+2×1000+25<2025+
+
+
+…+
=2025+100×
+900×
=2033<45.12,故可得证.
| |P1A1|2 |
| 2 |
(x0+
| ||
| 2 |
| 1 | ||
2
|
| |P2A2|2 |
| 2 |
| (y2-y1)2 |
| 2 |
(y1+
| ||
| 2 |
| 1 | ||
2
|
(2)由图可知An(yn-1,yn-1),,进而可得Sn=
| |PnAn|2 |
| 2 |
| (yn-yn-1)2 |
| 2 |
(yn-1+
| ||
| 2 |
| 1 | ||
2
|
由
| y | 2 n |
| y | 2 n-1 |
| 1 | ||
|
| y | 2 n |
| y | 2 n-1 |
| 1 | ||
|
| y | 2 n-1 |
| y | 2 n-2 |
| 1 | ||
|
(3)由(2)
| y | 2 1000 |
| T | 2 1000 |
| y | 2 100 |
| T | 2 100 |
| y | 2 1000 |
| T | 2 1000 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| 25 |
| 1 |
| 225 |
解答:(1)解:显然△A1P1A2为等腰直角三角形
S1=
=
=
同理S2=
=
=
=
(2)证明:由图可知An(yn-1,yn-1),∴yn=yn-1+
Sn=
=
=
=
由
=
+
+2得
-
=
+2,
-
=
+2
∴
-
=
+2
∴
-
=
+
+…+
+2n=2Tn+2n
∴yn2=2Tn+2n+x02;
(3)证明:由(2)
=2
+2×1000+25>2025>452
=2
+2×100+25>225
∵yn=yn-1+
∴
=2
+2×1000+25=2025+
+
+…+
<2025+
+
+
+…+
=2025+100×
+900×
=2033<45.12
∴45<y1000<45.1.
S1=
| |P1A1|2 |
| 2 |
(x0+
| ||
| 2 |
| 1 | ||
2
|
同理S2=
| |P2A2|2 |
| 2 |
| (y2-y1)2 |
| 2 |
(y1+
| ||
| 2 |
| 1 | ||
2
|
(2)证明:由图可知An(yn-1,yn-1),∴yn=yn-1+
| 1 |
| yn-1 |
Sn=
| |PnAn|2 |
| 2 |
| (yn-yn-1)2 |
| 2 |
(yn-1+
| ||
| 2 |
| 1 | ||
2
|
由
| y | 2 n |
| y | 2 n-1 |
| 1 | ||
|
| y | 2 n |
| y | 2 n-1 |
| 1 | ||
|
| y | 2 n-1 |
| y | 2 n-2 |
| 1 | ||
|
∴
| y | 2 1 |
| x | 2 0 |
| 1 | ||
|
∴
| y | 2 n |
| x | 2 0 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
∴yn2=2Tn+2n+x02;
(3)证明:由(2)
| y | 2 1000 |
| T | 2 1000 |
| y | 2 100 |
| T | 2 100 |
∵yn=yn-1+
| 1 |
| yn-1 |
∴
| y | 2 1000 |
| T | 2 1000 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
<2025+
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| 25 |
| 1 |
| 225 |
∴45<y1000<45.1.
点评:本题的考点是数列与不等式的综合,考查数列{Sn}的前n项和,考查放缩法证明不等式,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目