题目内容
探究函数f(x)=2x+ -3,x∈(0,+∞)上的最小值,并确定取得最小值时x的值.列表如下:
-3,x∈(0,+∞)上的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 14 | 7 | 5.33 | 5.11 | 5.01 | 5 | 5.01 | 5.04 | 5.08 | 5.67 | 7 | 8.6 | 12.14 | … |
(1)观察表中y值随x值变化趋势的特点,请你直接写出函数f(x)=2x+ -3在区间(0,+∞)上的单调区间,并指出f(x)的最小值及此时x的值.
-3在区间(0,+∞)上的单调区间,并指出f(x)的最小值及此时x的值.
(2)用单调性的定义证明函数f(x)=2x+ -3在区间(0,2]上的单调性;
-3在区间(0,2]上的单调性;
(3)设函数f(x)=2x+ -3在区间(0,a]上的最小值为g(a),求g(a)的表达式.
-3在区间(0,a]上的最小值为g(a),求g(a)的表达式.
(1)由表中可知f(x)在(0,2]为减函数,[2,+∞)为增函数,
并且当x=2时,f(x)min=5. ……5分
(2)证明:设0<x1<x2≤2,
因为f(x1)-f(x2)=2x1+ -3-(2x2+
-3-(2x2+ -3)=2(x1-x2)+
-3)=2(x1-x2)+ =
= ,
,
因为0<x1<x2≤2,所以x1-x2<0,0<x1x2<4,即x1x2-4<0.
所以f(x1)-f(x2)>0,即f(x1)>f(x2).
所以f(x)在(0,2]为减函数. ……10分
(3)由(2)可证:函数f(x)=2x+ -3在区间(0,2]上单调递减,在区间[2,+∞)上单调递增.则
-3在区间(0,2]上单调递减,在区间[2,+∞)上单调递增.则
①当0<a<2时,(0,a]⊆(0,2],所以函数f(x)=2x+ -3在区间(0,a]上单调递减,
-3在区间(0,a]上单调递减,
故f(x)min=f(a)=2a+ -3;
-3;
②当a≥2时,函数f(x)=2x+ -3在区间(0,2]上单调递减,[2,a]上单调递增,
-3在区间(0,2]上单调递减,[2,a]上单调递增,
故f(x)min=f(2)=5;
综上所述,函数f(x)=2x+ -3在区间(0,a]上的最小值为
-3在区间(0,a]上的最小值为
g(a)= ……16分
……16分

 满足
满足 ,则下面结论正确是 ( )
,则下面结论正确是 ( ) B.
B. C.
C. D.
D.
 则
则 的值为 .
的值为 .  ,则
,则 的单调递减区间是 .
的单调递减区间是 .  同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意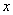 ,恒有
,恒有
 ,当
,当 时,恒有
时,恒有 ,则称函数
,则称函数 ;②
;② ; ③
; ③ ;
; ,能被称为“理想函数”的有 (填相应的序号).
,能被称为“理想函数”的有 (填相应的序号). = .
= . =
= (a,b,c分别为角A,B,C的对边),则△ABC的形状为 ____.
(a,b,c分别为角A,B,C的对边),则△ABC的形状为 ____. 
 中,若
中,若 ,则
,则 为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为 .
为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为 .