题目内容
已知:f(x)是定义在R上的不恒为零的函数,且对任意a、b∈R,满足:f(a•b)=af(b)+bf(a),且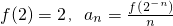 ,则数列{an}的通项公式an=________.
,则数列{an}的通项公式an=________.
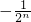
分析:令a=2-n,b=2,得f(2-n+1)=2-nf(2)+2f(2-n),设An=f(2-n),可得An-1=2-n-1+2An,从而可知数列{
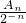 }是以-1为,-1为首项的等差数列,故可求数列{An}的通项公式,从而得出数列{an}的通项公式.
}是以-1为,-1为首项的等差数列,故可求数列{An}的通项公式,从而得出数列{an}的通项公式.解答:令a=1,b=1,得f(1)=f(1)+f(1),∴f(1)=0,
令a=2,b=
 ,得f(1)=2f(
,得f(1)=2f( )+
)+ f(2),且f(2)=2,∴f(
f(2),且f(2)=2,∴f( )=-
)=- ,
,令a=2-n,b=2,得f(2-n+1)=2-nf(2)+2f(2-n)
设An=f(2-n)
∴An-1=2-n-1+2An,
∴
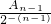 =1+
=1+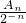 ,即
,即 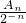 -
-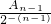 =-1,且
=-1,且  =
=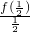 =-1
=-1即数列{
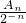 }是以-1为,-1为首项的等差数列
}是以-1为,-1为首项的等差数列∴
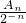 =-n,
=-n,∴An=-n•2-n
∴
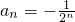 .
.故答案为:
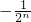 .
.点评:本题考查数列的函数特性、等差数列的定义,涉及抽象函数的应用,属中档题.

练习册系列答案
相关题目