题目内容

是否存在角θ，使得α、β是关于x的二次方程x2+2(cosθ+1)x+cos2θ=0的两根，且|α-β|≤22?若存在，求出角θ的取值范围；若不存在，请说明理由.

解:∵方程有两实根，

∴Δ=4(cosθ+1)2-4(cosθ)2≥0，

∴cosθ≥-.①

由韦达定理,得α+β=-2(cosθ+1)，

α·β=cos2θ，代入|α-β|≤2,得

4(cosθ+1)2-4(cosθ)2≤8，

即cosθ≤.②

由①②得-≤cosθ≤，

利用三角函数线可得θ角的范围为+2kπ≤θ≤+2kπ或+2kπ≤θ≤+2kπ(k∈Z).

故+kπ≤θ≤+kπ(k∈Z).

练习册系列答案
相关题目
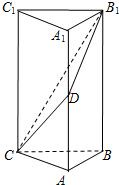精英家教网如图，在直三棱柱ABC-A1B1C1中，AB⊥BC，AB=BC=1，AA1=2，D是AA1的中点．
（Ⅰ）求异面直线A1C1与B1D所成角的大小；
（Ⅱ）求二面角C-B1D-B的大小；
（Ⅲ）在B1C上是否存在一点E，使得DE∥平面ABC？若存在，求出
B1EEC
的值；若不存在，请说明理由．
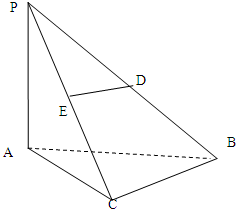精英家教网如图在三棱锥P-ABC中，PA⊥底面ABC，PA=AB，∠ABC=60°，∠BCA=90°，点D，E分别在棱PB，PC上，且DE∥BC，
（1）求证：BC⊥平面PAC
（2）当D为PB中点时，求AD与平面PAC所成的角的余弦值；
（3）是否存在点E，使得二面角A-DE-P为直二面角，并说明理由．
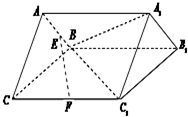如图，三棱柱ABC-A1B1C1中，BC=2，BC1=
2
，CC1=
2
，△ABC是以BC为底边的等腰三角形，平面ABC⊥平面BCC1B1，E为棱AB的中点，F为CC1上的动点．
（Ⅰ）在线段CC1上是否存在一点F，使得EF∥平面A1BC1？若存在，确定其位置；若不存在，说明理由．
（Ⅱ）在线段CC1上是否存在一点F，使得EF⊥BB1？若存在，确定其位置；若不存在，说明理由．
（ III）当F为CC1的中点时，若AC≤CC1，且EF与平面ACC1A1所成的角的正弦值为
2
3
，求二面角C-AA1-B的余弦值．
已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．
（Ⅰ）证明：BN⊥平面C1B1N；
（Ⅱ）设直线C1N与平面CNB1所成的角为θ，求cosθ的值；
（Ⅲ）M为AB中点，在CB上是否存在一点P，使得MP∥平面CNB1，若存在，求出BP的长；若不存在，请说明理由．
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，E、F分别为棱BC、AD的中点，PD⊥底面ABCD，且直线PA与直线BC所成的角为45°．
（Ⅰ）求证：DE∥平面PFB；
（Ⅱ）求四棱锥P-ABCD的体积．
（Ⅲ）在线段PB上是否存在点Q，使得FQ⊥面PBC？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网