题目内容
已知数列{an}的前n项和Sn与通项an之间满足a1=1,Sn=n2an,求an.
思路分析:本题除给出初始条件a1=1之外,还给了前n项和Sn与通项an之间的关系式Sn=n2an.为求an,需考虑使用公式an=Sn-Sn-1,从而把Sn与Sn-1之间的关系转化为an与an-1之间的递推关系.
解:当n≥2时,
Sn-Sn-1=n2an-(n-1)2an-1=an,
(n2-1)an=(n-1)2an-1,
(n+1)an=(n-1)an-1,
∴![]() =
=![]() .
.
∴![]() ·
·![]() ·
·![]() ·…·
·…·![]() ·
·![]() ·
·![]() =
=![]() ·
·![]() ·
·![]() ·…·
·…·![]() ·
·![]() ·
·![]() ,=
,=![]() =
=![]() .
.
又由S2=a1+a2=22·a2![]()
![]() ,
,
∴an=![]() (n≥2).此通项公式对n=1也成立.
(n≥2).此通项公式对n=1也成立.
∴an=![]() .
.

练习册系列答案
相关题目
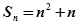 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________
 ,那么它的通项公式为an=_________
.
,那么它的通项公式为an=_________
. , 则数列的通项an=
, 则数列的通项an=