题目内容
四棱锥A-BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC＝2，CD＝
，AB=AC.
(1) 证明：AD⊥CE;
(2) 设侧面ABC为等边三角形，求二面角C-AD-E的大小.
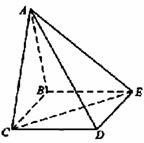
解：（1）取BC中点F，连接DF交CE于点O
∵AB=AC
∴AF⊥BC
又面ABC⊥面BCDE
∴AF⊥面BCDE
∴AF⊥CE
∴∠OED+∠ODE+90°
∴∠DOE=90°即CE⊥DF
∴CE⊥面ADF
∴CE⊥AD
(2)在面ACD内过C点做AD的垂线，垂足为G
∵CG⊥AD CE⊥AD
∴AD⊥面CEG
∴EG⊥AD
则∠CGB即为所求二面角
则
练习册系列答案
相关题目
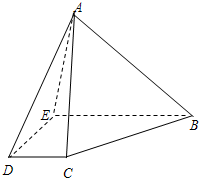如图，在四棱锥A-BCDE中，底面BCDE是直角梯形，∠BED=90°，BE∥CD，AB=6，BC=5，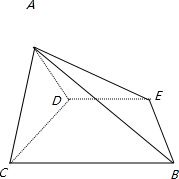
如图，四棱锥A-BCDE中，△ABC是正三角形，四边形BCDE是矩形，且平面ABC⊥平面BCDE，AB=2，AD=4．
如图，四棱锥A-BCDE中，△ABC是正三角形，四边形BCDE是矩形，且平面ABC⊥平面BCDE，AB=2，AD=4．
如图，四棱锥A-BCDE中，侧面△ADE是等边三角形，在底面等腰梯形BCDE中，CD∥BE，DE=2，CD=4，∠CDE=60°，M为DE的中点，F为AC的中点，AC=4．