题目内容
(2013•盐城一模)已知函数f(x)=
,若关于x的方程f(x)=kx(k>0)有且仅有四个根,其最大根为t,则函数g(t)=
t2-6t+7的值域为
|
| 25 |
| 24 |
[-
,-1)
| 41 |
| 25 |
[-
,-1)
.| 41 |
| 25 |
分析:同一坐标系内作出函数y=f(x)的图象和直线y=kx,因为两图象有且仅有四个公共点,得出最大根t的取值范围.再利用二次函数的性质,即可得到函数g(t)=
t2-6t+7的值域.
| 25 |
| 24 |
解答: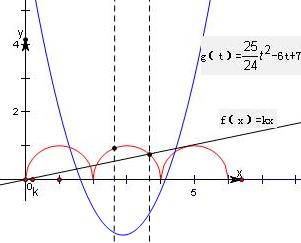 解:作出函数f(x)=
解:作出函数f(x)=
,当0≤x<4时的图象,如右图中红色的三个半圆.
将直线y=kx围绕坐标原点进行旋转,可得当直线介于与第二个半圆相切和与第三个半圆相切之间时,两图象有且仅有四个不同的公共点,
此时,其最大根t∈(
,
),
则函数g(t)=
t2-6t+7,t∈(
,
)的值域为[-
,-1).
故答案为:[-
,-1).
 解:作出函数f(x)=
解:作出函数f(x)=
|
将直线y=kx围绕坐标原点进行旋转,可得当直线介于与第二个半圆相切和与第三个半圆相切之间时,两图象有且仅有四个不同的公共点,
此时,其最大根t∈(
| 8 |
| 3 |
72+8
| ||
| 25 |
则函数g(t)=
| 25 |
| 24 |
| 8 |
| 3 |
72+8
| ||
| 25 |
| 41 |
| 25 |
故答案为:[-
| 41 |
| 25 |
点评:本题以分段函数为例,求方程的最大根,并且用这个根来求值域,着重考查了函数与方程的关系,以及数形结合思想,属于中档题.

练习册系列答案
相关题目
 (2013•盐城一模)如图,在等腰三角形ABC中,底边BC=2,
(2013•盐城一模)如图,在等腰三角形ABC中,底边BC=2,