题目内容
已知函数f(x)=x-1-alnx(a∈R),
(1)若曲线y=f(x)在x=1处的切线的方程为3x-y-3=0,求实数a的值;
(2)求证:f(x)≥0恒成立的充要条件是a=1;
(3)若a<0,且对任意x1,x2∈(0,1],都有|f(x1)-f(x2)|≤4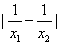 ,求实数a的取值范围。
,求实数a的取值范围。
(1)若曲线y=f(x)在x=1处的切线的方程为3x-y-3=0,求实数a的值;
(2)求证:f(x)≥0恒成立的充要条件是a=1;
(3)若a<0,且对任意x1,x2∈(0,1],都有|f(x1)-f(x2)|≤4
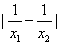 ,求实数a的取值范围。
,求实数a的取值范围。 解:(1)因为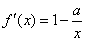 ,所以f′(1)=1-a,
,所以f′(1)=1-a,
所以曲线y=f(x)在x=1处切线的斜率为1-a,
因为曲线y=f(x)在x=1处的切线为3x-y-3=0,
所以1-a=3,解得a=-2;
(2)①充分性,当a=1时,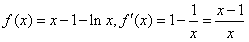 ,
,
所以当x>1时,f′(x)>0,所以函数f(x)在(1,+∞)上是增函数;
当0<x<1时,f′(x)<0,所以函数f(x)在(0,1)上是减函数,
所以f(x)≥f(1)=0;
②必要性: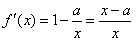 ,其中x>0,
,其中x>0,
(ⅰ)当a≤0时,因为f′(x)>0恒成立,所以函数f(x)在(0,+∞)上是增函数;
而f(1)=0,所以当x∈(0,1)时,f(x)<0,与f(x)≥0恒成立相矛盾,所以a≤0不满足题意;
(ⅱ)当a>0时,因为当x>a时,f′(x)>0,所以函数f(x)在(a,+∞)上是增函数;
当0<x<a时,f′(x)<0,所以函数f(x)在(0,a)上是减函数,
所以f(x)≥f(a)=a-1-alna,
因为f(1)=0,所以当a≠1时,f(a)<f(1)=0,此时与f(x)≥0恒成立相矛盾,
所以a=1;
综上所述f(x)≥0恒成立的充要条件是a=1;
(3)由(2)可知,当a<0时,函数f(x)在(0,1]上是增函数,
又函数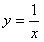 在(0,1]上是减函数,
在(0,1]上是减函数,
不妨设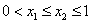 ,
,
则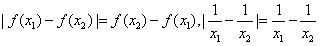 ,
,
所以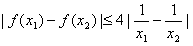 等价于
等价于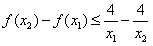 ,
,
即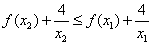 ,
,
设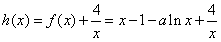 ,
,
则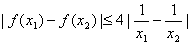 等价于函数h(x)在区间(0,1]上是减函数,
等价于函数h(x)在区间(0,1]上是减函数,
因为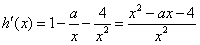 ,
,
所以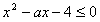 在x∈(0,1]上恒成立,
在x∈(0,1]上恒成立,
即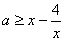 在x∈(0,1]上恒成立,即a不小于
在x∈(0,1]上恒成立,即a不小于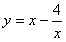 在区间(0,1]内的最大值,
在区间(0,1]内的最大值,
而函数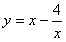 在区间(0,1]上是增函数,
在区间(0,1]上是增函数,
所以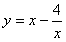 的最大值为-3,
的最大值为-3,
所以a≥-3,
又a<0,所以a∈[-3,0)。
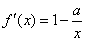 ,所以f′(1)=1-a,
,所以f′(1)=1-a,所以曲线y=f(x)在x=1处切线的斜率为1-a,
因为曲线y=f(x)在x=1处的切线为3x-y-3=0,
所以1-a=3,解得a=-2;
(2)①充分性,当a=1时,
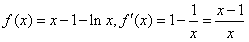 ,
,所以当x>1时,f′(x)>0,所以函数f(x)在(1,+∞)上是增函数;
当0<x<1时,f′(x)<0,所以函数f(x)在(0,1)上是减函数,
所以f(x)≥f(1)=0;
②必要性:
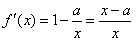 ,其中x>0,
,其中x>0,(ⅰ)当a≤0时,因为f′(x)>0恒成立,所以函数f(x)在(0,+∞)上是增函数;
而f(1)=0,所以当x∈(0,1)时,f(x)<0,与f(x)≥0恒成立相矛盾,所以a≤0不满足题意;
(ⅱ)当a>0时,因为当x>a时,f′(x)>0,所以函数f(x)在(a,+∞)上是增函数;
当0<x<a时,f′(x)<0,所以函数f(x)在(0,a)上是减函数,
所以f(x)≥f(a)=a-1-alna,
因为f(1)=0,所以当a≠1时,f(a)<f(1)=0,此时与f(x)≥0恒成立相矛盾,
所以a=1;
综上所述f(x)≥0恒成立的充要条件是a=1;
(3)由(2)可知,当a<0时,函数f(x)在(0,1]上是增函数,
又函数
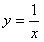 在(0,1]上是减函数,
在(0,1]上是减函数,不妨设
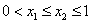 ,
,则
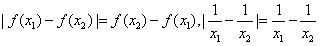 ,
,所以
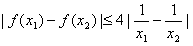 等价于
等价于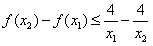 ,
,即
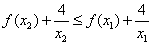 ,
,设
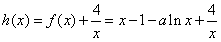 ,
,则
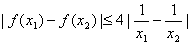 等价于函数h(x)在区间(0,1]上是减函数,
等价于函数h(x)在区间(0,1]上是减函数,因为
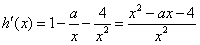 ,
,所以
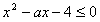 在x∈(0,1]上恒成立,
在x∈(0,1]上恒成立,即
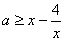 在x∈(0,1]上恒成立,即a不小于
在x∈(0,1]上恒成立,即a不小于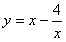 在区间(0,1]内的最大值,
在区间(0,1]内的最大值,而函数
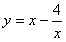 在区间(0,1]上是增函数,
在区间(0,1]上是增函数,所以
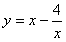 的最大值为-3,
的最大值为-3,所以a≥-3,
又a<0,所以a∈[-3,0)。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目