题目内容
已知正四棱柱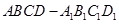 中
中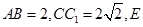 为
为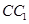 的中点,则直线
的中点,则直线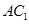 与平面
与平面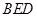 的距离为( )
的距离为( )
A.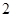 B.
B.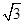 C.
C.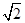 D.
D.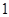
【答案】
D
【解析】
试题分析:如图:连接AC,交BD于O,在三角形CC1A中,易证OE∥C1A,

从而C1A∥平面BDE,∴直线AC1与平面BED的距离即为点A到平面BED的距离,设为h.
在三棱锥E-ABD中,VE-ABD= 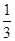 S△ABD×EC=
S△ABD×EC= 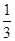 ×
×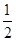 ×2×2
×2×2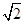 =
=  .
.
在三棱锥A-BDE中,BD=2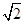 ,BE=
,BE=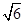 ,DE=
,DE=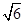 ,∴S△EBD=
,∴S△EBD=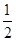 ×2
×2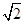 ×2=2
×2=2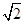 .
.
∴VA-BDE=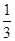 ×S△EBD×h=
×S△EBD×h=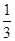 ×2
×2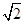 ×h=
×h= ,∴h=1,
,∴h=1,
故选 D.
考点:正四棱柱的几何特征,距离计算。
点评:中档题,涉及立体几何中距离计算问题,要充分借助于几何体的特征,并注意距离的“转化”。本题利用“体积法”计算距离,值得学习。

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 (2006•崇文区二模)如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长为
(2006•崇文区二模)如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长为  中,
中, =
= ,
, 为
为 与
与 所形成角的余弦值为
所形成角的余弦值为