题目内容
 如图:点P是⊙O直径AB延长线上一点,PC是⊙O的切线,C是切点,AC=4,BC=3,则PC=
如图:点P是⊙O直径AB延长线上一点,PC是⊙O的切线,C是切点,AC=4,BC=3,则PC=| 60 |
| 7 |
| 60 |
| 7 |
分析:先通过△PCB≌△PAC得出 PC=
PA,又 PC2=PB•PA,所以(
PA)2=PB•PA,得出PB=
PA,求出PB,PA后即可求出PC
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 16 |
解答:解:根据弦切角定理得知,∠PCB=∠PAC,△PCB≌△PAC.
∴
=
=
=
,PC=
PA,
又 PC2=PB•PA,
所以(
PA)2=PB•PA,得出PB=
PA,而直径AB=5,
所以上式化为PB=
(PB+5)
所以PB=
,PA=
,PC=
=
故答案为:
∴
| PC |
| PA |
| PB |
| PC |
| BC |
| AC |
| 3 |
| 4 |
| 3 |
| 4 |
又 PC2=PB•PA,
所以(
| 3 |
| 4 |
| 9 |
| 16 |
所以上式化为PB=
| 9 |
| 16 |
所以PB=
| 45 |
| 7 |
| 80 |
| 7 |
| PB•PA |
| 60 |
| 7 |
故答案为:
| 60 |
| 7 |
点评:本题考查与圆有关的线段长度求解,用到了切线长定理.应熟练掌握:1.射影定理的内容及其证明; 2.圆周角与弦切角定理的内容及其证明;3.圆幂定理的内容及其证明;4.圆内接四边形的性质与判定.

练习册系列答案
相关题目
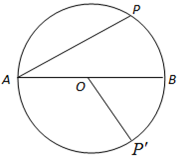 如图,点P是以AB为直径的圆O上动点,P'是点P关于AB的对称点,AB=2a(a>0).
如图,点P是以AB为直径的圆O上动点,P'是点P关于AB的对称点,AB=2a(a>0).

 如图:点P是⊙O直径AB延长线上一点,PC是⊙O的切线,C是切点,AC=4,BC=3,则PC= .
如图:点P是⊙O直径AB延长线上一点,PC是⊙O的切线,C是切点,AC=4,BC=3,则PC= . O直径AB延长线上一点,PC是
O直径AB延长线上一点,PC是 O的切线,C是切点,AC=4,BC=3,
O的切线,C是切点,AC=4,BC=3,