题目内容
双曲线 的两焦点为F1,F2,P点在双曲线上,且满足|PF1|+|PF2|=2
的两焦点为F1,F2,P点在双曲线上,且满足|PF1|+|PF2|=2 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( )A.2
B.1
C.4
D.3
【答案】分析:不妨假设P点在双曲线的右支上,利用双曲线的定义及|PF1|+|PF2|=2 ,求得|PF1|、|PF2|,从而可求△PF1F2的面积则△PF1F2的面积.
,求得|PF1|、|PF2|,从而可求△PF1F2的面积则△PF1F2的面积.
解答:解:不妨假设P点在双曲线的右支上,则|PF1|-|PF2|=2 ,
,
∵|PF1|+|PF2|=2 ,
,
∴|PF1|= ,|PF2|=
,|PF2|= -
- ,
,
∵|F1F2|=4,∴|PF1|2+|PF2|2=|F1F2|2,
∴△PF1F2的面积为 |PF1||PF2|=1
|PF1||PF2|=1
故选B.
点评:本题考查双曲线的定义,考查三角形面积的计算,考查学生的计算能力,属于基础题.
 ,求得|PF1|、|PF2|,从而可求△PF1F2的面积则△PF1F2的面积.
,求得|PF1|、|PF2|,从而可求△PF1F2的面积则△PF1F2的面积.解答:解:不妨假设P点在双曲线的右支上,则|PF1|-|PF2|=2
 ,
,∵|PF1|+|PF2|=2
 ,
,∴|PF1|=
 ,|PF2|=
,|PF2|= -
- ,
,∵|F1F2|=4,∴|PF1|2+|PF2|2=|F1F2|2,
∴△PF1F2的面积为
 |PF1||PF2|=1
|PF1||PF2|=1故选B.
点评:本题考查双曲线的定义,考查三角形面积的计算,考查学生的计算能力,属于基础题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
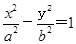 的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是
的两焦点为F1、F2,点P在双曲线上,∠F1PF2的平分线分线段F1F2的比为5 :1,则双曲线离心率的取值范围是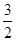 ]
B.(1,
]
B.(1,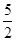 ] D.(
] D.( 的两焦点为F1,F2,过F2作x轴的垂线交双曲线于A,B两点,若△ABF1内切圆的半径为a,则此双曲线的离心率为( )
的两焦点为F1,F2,过F2作x轴的垂线交双曲线于A,B两点,若△ABF1内切圆的半径为a,则此双曲线的离心率为( )
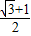


 的两焦点为F1,F2,P点在双曲线上,且满足|PF1|+|PF2|=2
的两焦点为F1,F2,P点在双曲线上,且满足|PF1|+|PF2|=2 ,则△PF1F2的面积为( )
,则△PF1F2的面积为( ) 的两焦点为F1,F2,P为动点,若PF1+PF2=4.
的两焦点为F1,F2,P为动点,若PF1+PF2=4.