题目内容
若对于任意实数x,都有 ,则a3的值为________.
,则a3的值为________.
-8
分析:把 x4=[-2+(x+2)]4 展开求得(x+2)3的系数,再结合已知条件求得a3的值.
解答:∵x4=[-2+(x+2)]4= (-2)4 (x+2)0+
(-2)4 (x+2)0+ (-2)3(x+2)1+
(-2)3(x+2)1+ (-2)2 (x+2)2+
(-2)2 (x+2)2+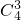 (-2)(x+2)3+
(-2)(x+2)3+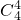 (-2)0(x+2)4,
(-2)0(x+2)4,
且有 ,
,
∴a3=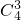 (-2)=-8,
(-2)=-8,
故答案为-8.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.
分析:把 x4=[-2+(x+2)]4 展开求得(x+2)3的系数,再结合已知条件求得a3的值.
解答:∵x4=[-2+(x+2)]4=
 (-2)4 (x+2)0+
(-2)4 (x+2)0+ (-2)3(x+2)1+
(-2)3(x+2)1+ (-2)2 (x+2)2+
(-2)2 (x+2)2+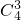 (-2)(x+2)3+
(-2)(x+2)3+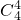 (-2)0(x+2)4,
(-2)0(x+2)4,且有
 ,
,∴a3=
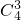 (-2)=-8,
(-2)=-8,故答案为-8.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 的图象关于直线
的图象关于直线 对称;
对称; >1,
>1, ,
, ,且
,且 在(-∞,0]上是减函数,
在(-∞,0]上是减函数, ;
; 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是 ;
;
 <f(2)
<f(2)