题目内容
A
 解:(1)因为PC^平面ABC,ABÌ平面ABC,
解:(1)因为PC^平面ABC,ABÌ平面ABC,
所以PC^AB. (1分)
因为CD^平面PAB,ABÌ平面PAB,
所以CD^AB. (2分)
又PCÇCD=C,所以AB^平面PCB. (4分)
(2)由(1)AB^平面PCB,所以AB^BC.
又PC=AC=2,AB=BC,所以![]() .
.
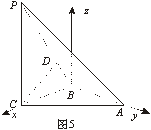
以B为原点,建立如图5所示的直角坐标系. (5分)
则A(0,![]() ,0),B(0,0,0),C(
,0),B(0,0,0),C(![]() ,0,0),P(
,0,0),P(![]() ,0,2). (6分)
,0,2). (6分)
于是,![]() ,
,![]() . (7分)
. (7分)
所以![]() , (8分)
, (8分)
故异面直线AP与BC所成的角为![]() . (9分)
. (9分)
(3)设平面PAB的法向量为![]() .
.
由![]() ,
,![]() ,
,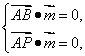
得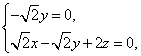
![]() 解得
解得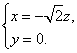
不妨令![]() , 得
, 得![]() . (11分)
. (11分)
设平面PAC的法向量为![]() .
.
由![]() ,
,![]() ,
,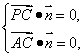
得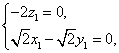 解得
解得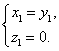
不妨令![]() ,得
,得 ![]() . (13分)
. (13分)
于是![]() ,
,
故二面角C-PA-B大小的余弦值为![]() . (14分)
. (14分)

练习册系列答案
相关题目
函数y=
-1(x≤0)的反函数是( )
| 3 | x2 |
A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
已知函数y=tanωx在(-
,
)上是减函数,则( )
| π |
| 2 |
| π |
| 2 |
| A、0<ω≤1 | B、-1≤ω<0 |
| C、ω≥1 | D、ω≤-1 |