题目内容
若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为
A. | B. | C. | D. |
B
解析试题分析:由题意,该三棱柱底面三角形边长为2,几何体高为1。其外接球球心是上下底面的连心线的中点,由平面几何知识,球半径r满足 ,所以,该球的表面积为
,所以,该球的表面积为
 ,选B。
,选B。
考点:三视图,三棱柱及其外接球的几何特征。
点评:小综合题,涉及三视图的题目,基本成为高考必考的知识内容,要注意掌握画法规则,准确地还原几何体,并利用几何体的特征解题。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
如图,正方体ABCD-A1B1C1D1的棱长为2,动点E、F在BC1上,动点P、Q分别在AD1、CD上,若 ,
, ,则四面体P-EFQ的体积( )
,则四面体P-EFQ的体积( )
| A.与x、y都有关 | B.与x有关、与y无关 |
| C.与x、y都无关 | D.与x无关、与y有关 |

一个几何体的三视图如图,该几何体的表面积是( ) 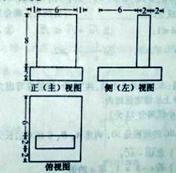
| A.372 | B.360 | C.292 | D.280 |
一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为( ) .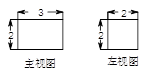
| A.长方形 |
| B.直角三角形 |
| C.圆 |
| D.椭圆 |
已知某几何体的三视图如图所示,那么这个几何体是( )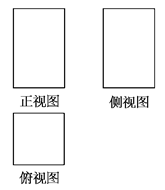
| A.长方体 | B.圆柱 | C.四棱锥 | D.四棱台 |
已知平面 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与 成
成 角的平面
角的平面 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4 、13
、13 ,则球面面积为
,则球面面积为
A.36 | B.48 | C.64 | D.100 |
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是
A. | B. | C. | D. |
 ,则这个圆锥的全面积是( )
,则这个圆锥的全面积是( )






