题目内容
求与两定圆x2+y2=1,x2+y2-8x-33=0都相切的动圆圆心的轨迹方程.分析:设出动圆圆心的坐标,依据内切和外切,动圆圆心到两个定圆的圆心的距离分别等于半径的和与差,来求得结果.
解答: 解:(1) 将⊙O1的x2+y2-8x-33=0方程化为(x-4)2+y2=49,
解:(1) 将⊙O1的x2+y2-8x-33=0方程化为(x-4)2+y2=49,
∴O1(4,0),r1=7,设动圆圆心为C(x,y).
由两圆相切时圆心距与两圆半径的关系,有:
7-|O1C|=|OC|-1
即O1C|+|OC|=8也就是说C点到点O1、O的距离之和等于8
由椭圆的定义知到C的轨迹是以(0,0)和(4,0)为焦点
长轴长为8的椭圆,a=4,c=2,b2=12
∴动圆圆心C的轨迹方程为
+
=1
(2)当动圆C与⊙O1和⊙O都内切时,由O1C|+|OC|=6同理可得
动圆圆心C的轨迹方程为
+
=1
综上动圆圆心C的轨迹方程为
+
=1或
+
=1
 解:(1) 将⊙O1的x2+y2-8x-33=0方程化为(x-4)2+y2=49,
解:(1) 将⊙O1的x2+y2-8x-33=0方程化为(x-4)2+y2=49,∴O1(4,0),r1=7,设动圆圆心为C(x,y).
由两圆相切时圆心距与两圆半径的关系,有:
7-|O1C|=|OC|-1
即O1C|+|OC|=8也就是说C点到点O1、O的距离之和等于8
由椭圆的定义知到C的轨迹是以(0,0)和(4,0)为焦点
长轴长为8的椭圆,a=4,c=2,b2=12
∴动圆圆心C的轨迹方程为
| (x-2)2 |
| 16 |
| y2 |
| 12 |
(2)当动圆C与⊙O1和⊙O都内切时,由O1C|+|OC|=6同理可得
动圆圆心C的轨迹方程为
| (x-2)2 |
| 9 |
| y2 |
| 5 |
综上动圆圆心C的轨迹方程为
| (x-2)2 |
| 16 |
| y2 |
| 12 |
| (x-2)2 |
| 9 |
| y2 |
| 5 |
点评:本题考查两圆的位置关系,考查转化的思想,是中档题.

练习册系列答案
相关题目
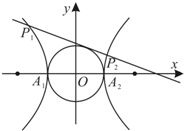 已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).
已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).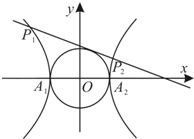 已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).
已知双曲线x2-y2=1的左、右顶点分别为A1、A2,动直线l:y=kx+m与圆x2+y2=1相切,且与双曲线左、右两支的交点分别为P1(x1,y1),P2(x2,y2).