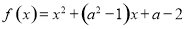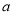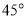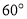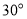题目内容
已知函数
是定义域为R的奇函数.当
时，
，图像如图所示.
（Ⅰ）求
的解析式；
（Ⅱ）若方程
有两解，写出
的范围；
（Ⅲ）解不等式
，写出解集.
（Ⅰ）
；
（Ⅱ）
；（Ⅲ）
【解析】
试题分析：（Ⅰ）当
时，
，即可代入
中得
，由奇函数的性质
，可得
，又因为奇函数中
，从而得到分段函数
的解析式；（Ⅱ）根据数形结合，使
的图像与直线
产生两个交点，容易看出
的取值范围；（Ⅲ）分
和
分别求解不等式的解集.
试题解析：（Ⅰ）
，
，
又
，
当
时，
2分
当时，，
，
，
即 4分
6分
（Ⅱ） 10分
（Ⅲ）①，
，
13分
②，
，
综上：解集为 16分
考点：奇函数的性质，数形结合思想，分类讨论思想.
练习册系列答案
相关题目
