题目内容
(本小题满分12分)
已知数列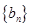 中,
中,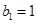 ,且点
,且点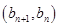 在直线
在直线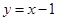 上.数列
上.数列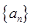 中,
中,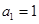 ,
,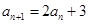 ,
,
(Ⅰ) 求数列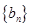 的通项公式(Ⅱ)求数列
的通项公式(Ⅱ)求数列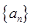 的通项公式;
的通项公式;
(Ⅲ)(理)若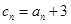 ,求数列
,求数列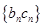 的前
的前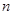 项和
项和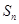 .
.
已知数列
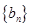 中,
中,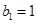 ,且点
,且点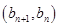 在直线
在直线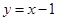 上.数列
上.数列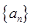 中,
中,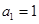 ,
,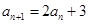 ,
,(Ⅰ) 求数列
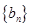 的通项公式(Ⅱ)求数列
的通项公式(Ⅱ)求数列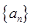 的通项公式;
的通项公式; (Ⅲ)(理)若
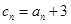 ,求数列
,求数列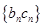 的前
的前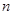 项和
项和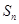 .
.(Ⅰ) 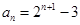 (n∈
(n∈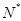 );(Ⅱ)
);(Ⅱ)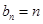 ;(Ⅲ)
;(Ⅲ)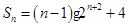 (n∈
(n∈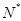 )
)
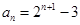 (n∈
(n∈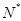 );(Ⅱ)
);(Ⅱ)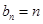 ;(Ⅲ)
;(Ⅲ)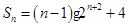 (n∈
(n∈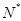 )
)本题考查数列的通项公式的计算和前n项和公式的求法,综合性强,难度大,容易出错.解题时要认真审题,注意错位相减法的灵活运用.
(Ⅰ)由an+1=2an+3得an+1+3=2(an+3),由此能求出an.
(Ⅱ)因为(bn+1,bn)在直线y=x-1上,所以bn=bn+1-1即bn+1-bn=1,由此能求出bn.
(Ⅲ)由cn=an+3=2n+1-3+3=2n+1,知bncn=n•2n+1,所以Sn=1×22+2×23+3×24+…+n•2n+1,再由错位相减法能求出Sn.
解:(Ⅰ)由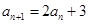 得
得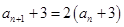
所以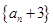 是首项为
是首项为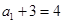 ,公比为2的等比数列.
,公比为2的等比数列.
所以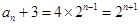 ,故
,故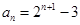 (n∈
(n∈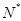 )
)
(Ⅱ)因为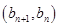 在直线
在直线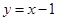 上,
上,
所以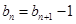 即
即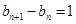 又
又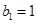
故数列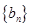 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
所以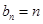
(Ⅲ)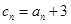 =
=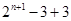 =
=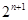 故
故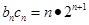
所以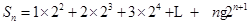
故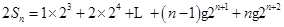
相减得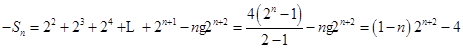
所以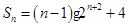 (n∈
(n∈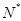 )
)
(Ⅰ)由an+1=2an+3得an+1+3=2(an+3),由此能求出an.
(Ⅱ)因为(bn+1,bn)在直线y=x-1上,所以bn=bn+1-1即bn+1-bn=1,由此能求出bn.
(Ⅲ)由cn=an+3=2n+1-3+3=2n+1,知bncn=n•2n+1,所以Sn=1×22+2×23+3×24+…+n•2n+1,再由错位相减法能求出Sn.
解:(Ⅰ)由
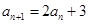 得
得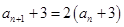
所以
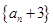 是首项为
是首项为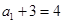 ,公比为2的等比数列.
,公比为2的等比数列.所以
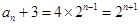 ,故
,故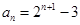 (n∈
(n∈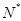 )
)(Ⅱ)因为
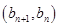 在直线
在直线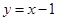 上,
上,所以
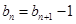 即
即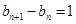 又
又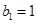
故数列
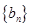 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,所以
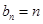
(Ⅲ)
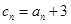 =
=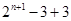 =
=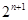 故
故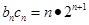
所以
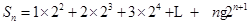
故
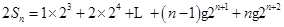
相减得
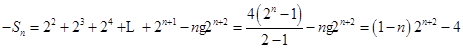
所以
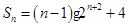 (n∈
(n∈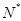 )
)
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
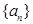 中
中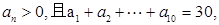 则
则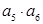 的最大值等于
的最大值等于 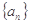 的前
的前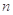 项和
项和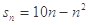 ,
,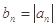 求 数列
求 数列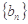 的前
的前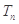 。
。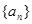 的前
的前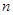 项和为
项和为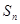 , 且
, 且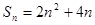 . 设数列
. 设数列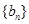 的前
的前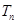 ,且
,且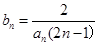 . (1)求
. (1)求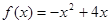 ,对(1)中的数列
,对(1)中的数列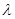 ,使得当
,使得当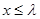 时,
时,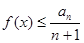 对任意
对任意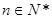 恒成立
恒成立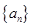 的前n项和为
的前n项和为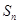 ,若
,若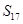 为一确定常数,则下列各式也为确定常数的是( )
为一确定常数,则下列各式也为确定常数的是( )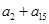
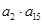
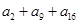
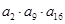
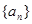 的前
的前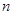 项和为
项和为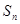 ,已知
,已知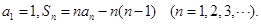
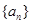 为等差数列,并写出
为等差数列,并写出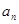 关于
关于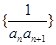 前
前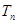 ,问满足
,问满足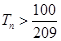 的最小正整数
的最小正整数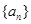 是一个公差为2的等差数列,
是一个公差为2的等差数列,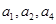 成等比数列.
成等比数列.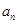 ;
;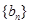 满足
满足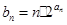 ,设
,设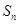 ,求
,求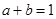 ,
,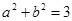 ,
,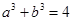 ,
,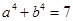 ,
, ,
,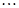 则
则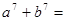 ( )
( )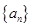 共有
共有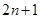 项,所有奇数项之和为
项,所有奇数项之和为 ,所有偶数项之和为
,所有偶数项之和为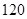 ,则n等于____________.
,则n等于____________.