题目内容
如图，在边长为a的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，PC=2a，E、F分别是PA和AB的中点．
（1）求证：EF∥面PBC；
（2）求证：平面PDB⊥平面PAC；
（3）求EF与平面PAC所成的角的正切值．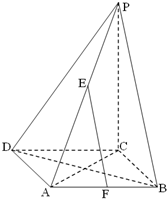
（1）求证：EF∥面PBC；
（2）求证：平面PDB⊥平面PAC；
（3）求EF与平面PAC所成的角的正切值．
（1）证明：∵AE=PE，AF=BF，∴EF∥PB
又 EF?平面PBC，PB?平面PBC，
∴EF∥平面PBC
（2）证明∵PC⊥面ABCD∴PC⊥BD
∵四边形ABCD为菱形∴AC⊥BD
又∵PC∩AC=C
∴BD⊥面PAC∵BD?面PBD
∴面PBD⊥面PCD
（3）记BD∩AC=O，连PO．由 （2）知BD⊥面PAC
又EF∥PB，∴∠BPO为EF与平面PAC所成的角
在△ABC中∵BC=a，∠ABC=60°，∴CO=
，BO=
a．
在Rt△POC中PO=
=
a，故 tan∠BPO=
=
所以直线EF与平面PAC所成的角的正切值为
又 EF?平面PBC，PB?平面PBC，
∴EF∥平面PBC
（2）证明∵PC⊥面ABCD∴PC⊥BD
∵四边形ABCD为菱形∴AC⊥BD
又∵PC∩AC=C
∴BD⊥面PAC∵BD?面PBD
∴面PBD⊥面PCD
（3）记BD∩AC=O，连PO．由 （2）知BD⊥面PAC
又EF∥PB，∴∠BPO为EF与平面PAC所成的角
在△ABC中∵BC=a，∠ABC=60°，∴CO=
| a |
| 2 |
| ||
| 2 |
在Rt△POC中PO=
| CO2+PC2 |
| ||
| 2 |
| BO |
| PO |
| ||
| 17 |
所以直线EF与平面PAC所成的角的正切值为
| ||
| 17 |
练习册系列答案
相关题目
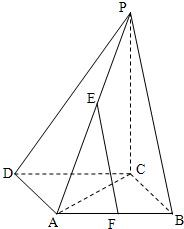如图，在边长为a的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，E，F是PA和AB的中点．
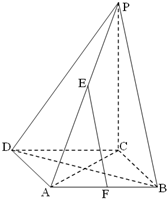如图，在边长为a的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，PC=2a，E、F分别是PA和AB的中点．
如图，在边长为a的菱形ABCD中，∠ABC=60°，PC丄平面ABCD，PC=
，E,F是PA和AB的中点。
，E,F是PA和AB的中点。