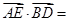题目内容
 如图,在边长为a的菱形ABCD中,∠ABC=60°,PC丄平面ABCD,PC=
如图,在边长为a的菱形ABCD中,∠ABC=60°,PC丄平面ABCD,PC=| 2 |
(1)求证:平面PBD丄平面PAC
(2)求三棱锥P-ECB的体积.
分析:(1)根据菱形的几何特征,及PC丄平面ABCD,可得BD⊥平面PAC,进而根据面面垂直的判定定理,得到平面PBD丄平面PAC
(2)由(1)中BD⊥平面PAC,即BD⊥平面PEC,即BD为三棱锥P-ECB的面PEC上的高,代入棱锥体积公式,可得答案.
(2)由(1)中BD⊥平面PAC,即BD⊥平面PEC,即BD为三棱锥P-ECB的面PEC上的高,代入棱锥体积公式,可得答案.
解答:证明:(1)在菱形ABCD中
BD⊥AC
∵PC丄平面ABCD,BD?平面ABCD,
∴PC丄BD
∵AC∩PC=C,AC,PC?平面PAC
∴BD⊥平面PAC,又∵BD?平面PBD
∴平面PBD丄平面PAC
(2)由(1)得BD丄平面PAC,即BD丄平面PEC
∵AC=a,∠ABC=60°
∴BD=
a
又∵PC=
a,E是PA的中点.
∴S△PAE=
•S△PAC=
a2
∴三棱锥P-ECB的体积V=
BD•S△PAE=
•
a•
a2=
a3

BD⊥AC
∵PC丄平面ABCD,BD?平面ABCD,
∴PC丄BD
∵AC∩PC=C,AC,PC?平面PAC
∴BD⊥平面PAC,又∵BD?平面PBD
∴平面PBD丄平面PAC
(2)由(1)得BD丄平面PAC,即BD丄平面PEC
∵AC=a,∠ABC=60°
∴BD=
| ||
| 2 |
又∵PC=
| 2 |
∴S△PAE=
| 1 |
| 2 |
| ||
| 4 |
∴三棱锥P-ECB的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 4 |
| ||
| 24 |
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积,(1)的关键是熟练掌握空间线线垂直,线面垂直及面面垂直的相互转化,(2)的关键是求出BD为三棱锥P-ECB的面PEC上的高.

练习册系列答案
相关题目
 (2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则
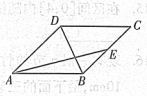
(2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则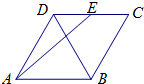 (2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则
(2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则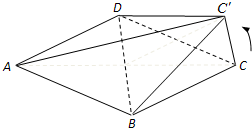 如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,折起后的点C记为C′,且CC′=a(
如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,折起后的点C记为C′,且CC′=a(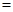
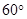 ,
,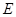 为
为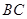 的中点,则
的中点,则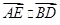
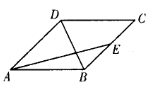
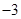 B.
B.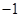 C.
C. D.
D.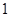
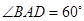 , E为BC中点,则
, E为BC中点,则