题目内容
在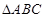 中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.(1)若
中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.(1)若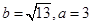 ,求边c的值;
,求边c的值;
(2)设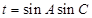 ,求t的最大值.
,求t的最大值.
(1) (2)
(2)
解析试题分析:(1)由三内角成等差可求 ,再利用余弦定理可求c;(2)由
,再利用余弦定理可求c;(2)由 ,可将
,可将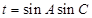 转化为
转化为 ,再由A范围求出最值.
,再由A范围求出最值.
试题解析:解:(1)因为角 成等差数列,所以
成等差数列,所以 ,
,
因为 ,所以
,所以 . 2分
. 2分
因为 ,
, ,
, ,
,
所以 .
.
所以 或
或 (舍去). 6分
(舍去). 6分
(2)因为 ,所以
,所以
 9分
9分
因为 ,所以
,所以 ,
,
所以当 ,即
,即 时,
时, 有最大值
有最大值 . 12分
. 12分
考点:等差数列,余弦定理, 的性质.
的性质.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 =(-cos
=(-cos ,sin
,sin =(cos
=(cos ,且
,且 .
.
 时,求二面角
时,求二面角 的余弦值.
的余弦值. 中,角
中,角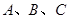 所对的边分别为
所对的边分别为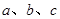 ,
,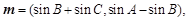
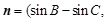
 ),且
),且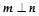 .
.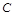 的大小;
的大小;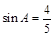 ,求
,求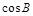 的值.
的值. 中,角
中,角 ,
, ,
, 所对的边分别是
所对的边分别是 ,
, ,
, ,若
,若 ,且
,且 ,求
,求 .
.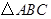 中,角A,B,C的对边分别为a,b,c,已知
中,角A,B,C的对边分别为a,b,c,已知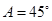 ,
, .
.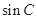 的值;
的值;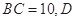 为
为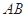 的中点,求
的中点,求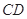 的长.
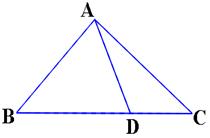
的长.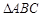 中,已知
中,已知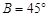 ,
,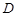 是
是 边上的一点,
边上的一点,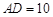 ,
,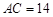 ,
,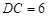 .
.
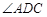 的大小;
的大小;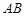 的长.
的长. ),且m⊥n.
),且m⊥n.