题目内容

定义：若函数f（x）对于其定义域内的某一数x0，有f（x0）=x0，则称x0是f（x）的一个不动点。
已知函数f（x）=ax2+(b+1)x+b-1(a≠0)。
(1) 当a=1，b=-2时，求函数f（x）的不动点；
(2) 若对任意的实数b，函数f（x）恒有两个不动点，求a的取值范围；
(3) 在(2)的条件下，若y=f（x）图象上两个点A、B的横坐标是函数f（x）的不动点，且A、 B的中点C在函数g（x）=-x+的图象上，求b的最小值。
（参考公式：A（x1，y1），B（x2，y2）的中点坐标为）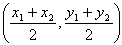

解：（1）f（x）=x2-x-3，
由x2-x-3=0，
解得x=3或x=-1，
所以所求的不动点为-1或3。
（2）令ax2+（b+1）x+b+1=x，
则ax2+bx+b-1=0，①
由题意，方程①恒由两个不等实根，
所以△=b2-4a（b-1）>0，
即b2-4ab+4a>0对任意的b∈R恒成立，
则△′=16a2-16a<0，故0<a<1。
（3）依题意，设，
则AB中点C的坐标为，
又AB的中点在直线上，
∴，
∴，
又x1，x2是方程①的两个根，
∴，
∴，
，
∴，
∴当时，bmin=-1。

练习册系列答案
相关题目
给出定义：若函数f（x）在D上可导，即f′（x）存在，且导函数f′（x）在D上也可导，则称f（x）在D上存在二阶导函数，记f″（x）=（f′（x））′，若f″（x）＜0在D上恒成立，则称f（x）在D上为凸函数．以下四个函数在(0，
π
2
)上不是凸函数的是（　　）
A、f（x）=sinx+cosx
B、f（x）=lnx-2x
C、f（x）=-x3+2x-1
D、f（x）=-xe-x
定义：若函数f（x）对于其定义域内的某一数x0，有 f （x0）=x0，则称x0是f （x）的一个不动点．已知函数f（x）=ax2+（b+1）x+b-1 （a≠0）．
（Ⅰ）当a=1，b=-2时，求函数f（x）的不动点；
（Ⅱ）若对任意的实数b，函数f（x）恒有两个不动点，求a的取值范围；
（Ⅲ）在（Ⅱ）的条件下，若y=f（x）图象上两个点A、B的横坐标是函数f（x）的不动点，且A、B两点关于直线y=kx+
a5a2-4a+1
对称，求b的最小值．
给出定义：若函数f（x）在D上可导，即f′（x）存在，且导函数f′（x）在D上也可导，则称f（x）在D上存在二阶导函数，记f″（x）=[（f′（x）]′．若f”（x）＞0在D上恒成立，则称f（x）在D上为凹函数．以下四个函数在(0，
π
2
)上不是 凹函数的是（　　）
A、f（x）=1-sinx
B、f（x）=ex-2x
C、f（x）=x3-x2-1
D、f（x）=-xe-x
（2011•广州模拟）定义：若函数f（x）的图象经过变换T后所得图象对应函数的值域与f（x）的值域相同，则称变换T是f（x）的同值变换．下面给出四个函数及其对应的变换T，其中T不属于f（x）的同值变换的是（　　）
给出定义：若函数f（x）在D上可导，即f′（x）存在，且导函数f′（x）在D上也可导，则称f（x）在D上存在二阶导函数，记f″（x）=（f′（x））′．若f″（x）＜0在D上恒成立，则称f（x）在D上为上凸函数．以下四个函数在(0，
π
2
)上不是上凸函数的是（　　）