题目内容
作函数y=tanx·cosx的图象.
解析:首先将函数的解析式变形,化为最简形式,然后作函数的图象.
当cosx≠0,即x≠
+kπ(k∈Z)时,有y=tanx·cosx=sinx,即y=sinx(x≠
+kπ,k∈Z).
其图象如图1-4-4.
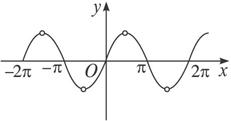
图1-4-4
点评:函数y=tanx·cosx的图象是y=sinx(x≠
+kπ,k∈Z)的图象,因此作出y=sinx的图象后,要把x=
+kπ(k∈Z)的这些点去掉.
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目