题目内容
已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且经过点P(1,
,且经过点P(1,![]() ).
).
 (1)求椭圆C的方程;
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为
圆心,MF为半径作圆M.问点M横坐标满足什么条
件时,圆M与y轴有两个交点?
(3)设圆M与y轴交于D、E两点,
求点D、E距离的最大值.
解:(1)∵椭圆![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且经过点P(1,
,且经过点P(1,![]() ),
),
∴ ,即
,即  ,解得
,解得 ![]() ,………………3分
,………………3分
∴椭圆C的方程为![]() +
+![]() =1。………………5分
=1。………………5分
(2)易求得F(1,0)。设M(x0,y0),则![]() +
+![]() =1, 圆M的方程为(x-x0)2+(y-y0)2=(1-x0)2+y02,
=1, 圆M的方程为(x-x0)2+(y-y0)2=(1-x0)2+y02,
令x=0,化简得y2-2y0y+2x0-1=0,⊿=4y02-4(2x0-1)2>0……①。
将y02=3(1-![]() )代入①,得3x02+8x0-16<0,解出 -4<x0<
)代入①,得3x02+8x0-16<0,解出 -4<x0<![]() 故-2≤x0<
故-2≤x0<![]() ……9分
……9分
(3)设D(0,y1),E(0,y2),其中y1<y2。由(2),得
DE= y2- y1=![]() =
=![]() =
=![]() ,
,
当x0=-![]() 时,DE的最大值为
时,DE的最大值为![]() 。………………15分
。………………15分

练习册系列答案
相关题目
 已知椭圆C:
已知椭圆C: +
+ =1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )
=1(a>b>0)的左右焦点为F1,F2,过F2线与圆x2+y2=b2相切于点A,并与椭圆C交与不同的两点P,Q,如图,PF1⊥PQ,若A为线段PQ的靠近P的三等分点,则椭圆的离心率为( )



 +
+ =1(a>b>0)的左、右焦点分别为F
=1(a>b>0)的左、右焦点分别为F 、F
、F ,A是椭圆C上的一点,AF
,A是椭圆C上的一点,AF
 +y
+y ,y
,y =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为
 :
: 与
与 轴交于点T,P为
轴交于点T,P为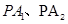 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,短轴一
,短轴一 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.