题目内容
已知圆C方程:(x-1)2+y2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且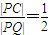 ;
;(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与x,y轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
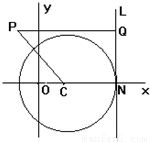
【答案】分析:(1)设出P点坐标,利用 ,建立方程,化简可得点P的轨迹方程;
,建立方程,化简可得点P的轨迹方程;
(2)先表示出四边形OADB的面积,利用辅助角公式化简,结合角的范围,即可求得结论.
解答:解:(1)设P点坐标为(x,y),则PQ=|4-x|,…(2分), …(3分)
…(3分)
因为 ,所以
,所以 ,…(4分)
,…(4分)
化简得 …(5分)
…(5分)
所以点P的轨迹方程是 …(6分)
…(6分)
(2)依题意得,A点坐标为(2,0),B点坐标为 …(7分)
…(7分)
设D点坐标为 ,…(8分)
,…(8分)
则四边形OADB的面积S四边形OADB=S△OAD+S△OBD= …(10分)
…(10分)
= =
= …(11分)
…(11分)
又因为 ,所以
,所以 …(12分)
…(12分)
所以 ,即
,即
所以四边形OADB的最大面积为 ,…(13分)
,…(13分)
当四边形OADB的面积取最大时, ,即
,即 ,
,
此时D点坐标为 …(14分)
…(14分)
点评:本题考查轨迹方程的求解,考查三角函数知识,考查学生的计算能力,正确表示四边形OADB的面积是关键.
 ,建立方程,化简可得点P的轨迹方程;
,建立方程,化简可得点P的轨迹方程;(2)先表示出四边形OADB的面积,利用辅助角公式化简,结合角的范围,即可求得结论.
解答:解:(1)设P点坐标为(x,y),则PQ=|4-x|,…(2分),
 …(3分)
…(3分)因为
 ,所以
,所以 ,…(4分)
,…(4分)化简得
 …(5分)
…(5分)所以点P的轨迹方程是
 …(6分)
…(6分)(2)依题意得,A点坐标为(2,0),B点坐标为
 …(7分)
…(7分)设D点坐标为
 ,…(8分)
,…(8分)则四边形OADB的面积S四边形OADB=S△OAD+S△OBD=
 …(10分)
…(10分)=
 =
= …(11分)
…(11分)又因为
 ,所以
,所以 …(12分)
…(12分)所以
 ,即
,即
所以四边形OADB的最大面积为
 ,…(13分)
,…(13分)当四边形OADB的面积取最大时,
 ,即
,即 ,
,此时D点坐标为
 …(14分)
…(14分)点评:本题考查轨迹方程的求解,考查三角函数知识,考查学生的计算能力,正确表示四边形OADB的面积是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•珠海二模)已知圆C方程:(x-1)2+y2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且
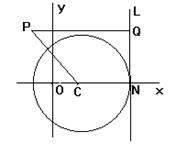
(2012•珠海二模)已知圆C方程:(x-1)2+y2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且 ;
;
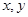 轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.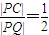 ;
;