题目内容
已知函数 ,
, .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)函数 在区间
在区间 上是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
上是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
解:(I) ,
, .
.
由 ,得
,得 ,或
,或 .
.
①当 ,即
,即 时,在
时,在 上,
上, ,
, 单调递减;
单调递减;
②当 ,即
,即 时,在
时,在 上,
上, ,
, 单调递增,在
单调递增,在 上,
上, ,
, 单调递减。
单调递减。
综上所述: 时,
时, 的减区间为
的减区间为 ;
;  时,
时, 的增区间为
的增区间为 ,
, 的减区间为
的减区间为 。
。
(II)(1)当 时,由(I)
时,由(I) 在
在 上单调递减,不存在最小值;
上单调递减,不存在最小值;
(2)当 时,
时,
若 ,即
,即 时,
时, 在
在 上单调递减,不存在最小值;
上单调递减,不存在最小值;
若 ,即
,即 时,
时, 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
因为 ,且当
,且当 时,
时, ,所以
,所以 时,
时, 。
。
又因为 ,所以当
,所以当 ,即
,即 时,
时, 有最小值
有最小值 ;
; ,即
,即 时,
时,  没有最小值。
没有最小值。
综上所述:当 时,
时, 有最小值
有最小值 ;当
;当 时,
时, 没有最小值。
没有最小值。

练习册系列答案
相关题目
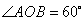 .若
.若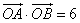 ,则
,则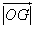 的最小值是________.
的最小值是________. 为锐角,若
为锐角,若 ,则
,则

 上递增 (B)在
上递增 (B)在 上递增,在
上递增,在 上递减
上递减  ,垂足为F.若
,垂足为F.若 ,
, ,则
,则 。
。
 ,
, .若
.若 ,则实数
,则实数 的值为
的值为  B.
B. C.
C. D.
D.
 中,
中,  ,
, ,
, 分别为角
分别为角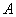 ,
,  ,C所对的边.已知角
,C所对的边.已知角 ,
, .
.



 若方程
若方程 有且仅有两个不等实根,且较大实根大于2,则实数
有且仅有两个不等实根,且较大实根大于2,则实数 的取值范围是 。
的取值范围是 。