题目内容
求下列函数的反函数 (1) ;(2)y=x|x|+2x;(3)
;(2)y=x|x|+2x;(3) ;(4)y=x3-3x2+3x+1;(5)y=log2(x2+1)(x<0)
;(4)y=x3-3x2+3x+1;(5)y=log2(x2+1)(x<0)
解:(1)∵y= ,
,
∴x2+x-y2=0,x≤-1,且y≥0.
∴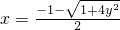 ,
,
x,y互换,得 的反函数为
的反函数为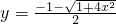 ,x≥0;
,x≥0;
(2)y=x|x|+2x,
当x≥0时,y=x2+2x,且y≥0,
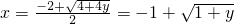 ,
,
x,y互换,得y=x2+2x的反函数为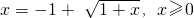 .
.
当x<0时,y=-x2+2x,且y<0,
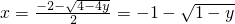 ,
,
x,y互换,得y=-x2+2x的反函数为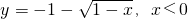 .
.
∴y=x|x|+2x的反函数为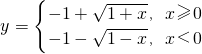 ;
;
(3) ,
,
当0≤x≤1时,y=x2-1∈[-1,0],
x2=y+1,
x= ,
,
x,y互换,得y=x2-1∈[-1,0]的反函数为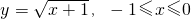 .
.
当-1≤x<0时,y=x2∈(0,1],
 ,
,
x,y互换,得y=x2∈(0,1]的反函数为 ,0<x≤1.
,0<x≤1.
∴ 的反函数
的反函数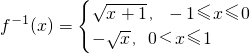 ;
;
(4)∵y=x3-3x2+3x+1,
∴y-2=x3-3x2+3x-1=(x-1)3,
x-1=(y-2) ,
,
∴x=(y-2) +1,
+1,
∴y=x3-3x2+3x+1的反函数是y=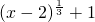 ,x∈R;
,x∈R;
(5)∵y=log2(x2+1)(x<0)
∴x2+1=2y,且y>0
x2=2y-1,
x=- ,
,
x,y互换,得y=log2(x2+1)(x<0)的反函数为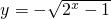 ,x>0.
,x>0.
分析:已知y=f(x),求y=f-1(x)的步骤:①把y看成常数,求出x:x=f-y;②x,y互换,得到y=f-1(x);③写出y=f-1(x)的定义域.由此利用题设条件,能够求出所给函数的反函数.
点评:本题考查反函数的求法,是基础题.解题时要认真审题,仔细解答,注意反函数定义域的求法.
 ,
,∴x2+x-y2=0,x≤-1,且y≥0.
∴
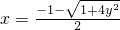 ,
,x,y互换,得
 的反函数为
的反函数为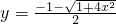 ,x≥0;
,x≥0;(2)y=x|x|+2x,
当x≥0时,y=x2+2x,且y≥0,
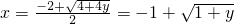 ,
,x,y互换,得y=x2+2x的反函数为
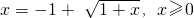 .
.当x<0时,y=-x2+2x,且y<0,
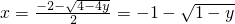 ,
,x,y互换,得y=-x2+2x的反函数为
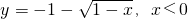 .
.∴y=x|x|+2x的反函数为
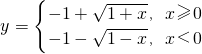 ;
;(3)
 ,
,当0≤x≤1时,y=x2-1∈[-1,0],
x2=y+1,
x=
 ,
,x,y互换,得y=x2-1∈[-1,0]的反函数为
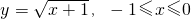 .
.当-1≤x<0时,y=x2∈(0,1],
 ,
,x,y互换,得y=x2∈(0,1]的反函数为
 ,0<x≤1.
,0<x≤1.∴
 的反函数
的反函数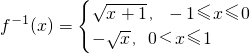 ;
;(4)∵y=x3-3x2+3x+1,
∴y-2=x3-3x2+3x-1=(x-1)3,
x-1=(y-2)
 ,
,∴x=(y-2)
 +1,
+1,∴y=x3-3x2+3x+1的反函数是y=
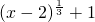 ,x∈R;
,x∈R;(5)∵y=log2(x2+1)(x<0)
∴x2+1=2y,且y>0
x2=2y-1,
x=-
 ,
,x,y互换,得y=log2(x2+1)(x<0)的反函数为
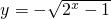 ,x>0.
,x>0.分析:已知y=f(x),求y=f-1(x)的步骤:①把y看成常数,求出x:x=f-y;②x,y互换,得到y=f-1(x);③写出y=f-1(x)的定义域.由此利用题设条件,能够求出所给函数的反函数.
点评:本题考查反函数的求法,是基础题.解题时要认真审题,仔细解答,注意反函数定义域的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )x
)x