题目内容
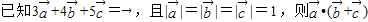=（ ）A．-
B．
C．-
D．-
【答案】分析：由条件判断 3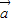
，4
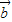，5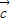
构成一个首尾相连接的直角三角形，把要求的式子化为 
•
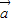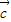=1×1cos＜
，
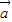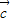＞，运算求得结果．
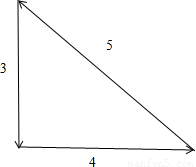
解答：解：∵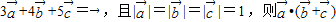
，
则 3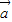
，4
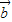，5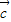
构成一个首尾相连接的直角三角形，如图所示：
∴
，
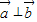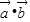=0，cos＜
＞=-
，
∴
=
+
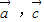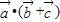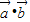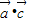=0+1×1×cos＜
＞=-
，
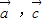故选 C．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的运算，判断 3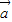
，4
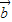，5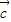
构成一个首尾相连接的直角三角形，是解题的关键，属于中档题．
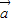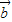，4，5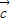构成一个首尾相连接的直角三角形，把要求的式子化为 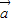•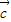=1×1cos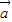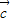＜，＞，运算求得结果．解答：解：∵
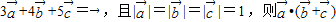，则 3
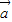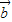，4，5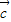构成一个首尾相连接的直角三角形，如图所示：∴
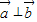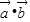，=0，cos＜＞=-，∴
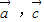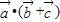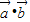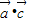=+=0+1×1×cos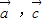＜＞=-，故选 C．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的运算，判断 3
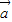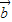，4，5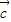构成一个首尾相连接的直角三角形，是解题的关键，属于中档题． 
练习册系列答案
相关题目
已知圆F的方程是x2+y2-2y=0，抛物线的顶点在原点，焦点是圆心F，过F引倾斜角为α的直线l，l与抛物线和圆依次交于A、B、C、D四点（在直线l上，这四个点从左至右依次为A、B、C、D），若|AB|，|BC|，|CD|成等差数列，则α的值为（ ）
A、±arctan
| ||||||||
B、
| ||||||||
C、arctan
| ||||||||
D、arctan
|
设函数f（x）=2+
（x≥0），则其反函数f-1（x）的图象是（ ）
| x |
A、 |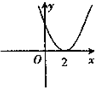
B、 |
C、 |
D、 |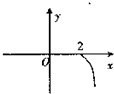
16、某人有4种颜色的灯泡（每种颜色的灯泡足够多），要在如图所示的6个点A、B、C、A1、B1、C1上各装一个灯泡，要求同一条线段两端的灯泡不同色，则每种颜色的灯泡都至少用一个的安装方法共有