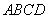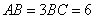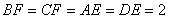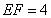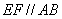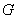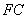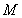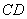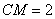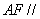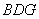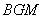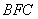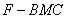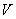题目内容
如图几何体中,四边形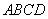 为矩形,
为矩形,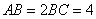 ,
,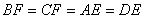 ,
,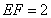 ,
,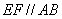 ,
,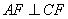 .
.

(1)若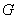 为
为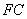 的中点,证明:
的中点,证明: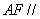 面
面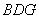 ;
;
(2)求二面角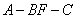 的余弦值.
的余弦值.
【答案】
(1)见解析;(2)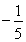 .
.
【解析】
试题分析:(1)连接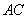 交
交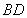 于
于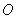 点,得知
点,得知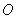 为
为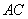 的中点,连接
的中点,连接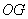
根据点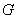 为
为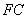 中点,利用三角形中位线定理,得出
中点,利用三角形中位线定理,得出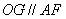 ,进一步得到
,进一步得到
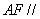 面
面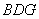 .
.
(2)首先探究几何体中的线面、线线垂直关系,创造建立空间直角坐标系的条件,应用“向量法”,确定二面角的余弦值.
解答本题的关键是确定“垂直关系”,这也是难点所在,平时学习中,应特别注意转化意识的培养,能从“非规范几何体”,探索得到建立空间直角坐标系的条件.
试题解析:(1)连接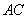 交
交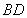 于
于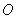 点,则
点,则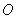 为
为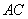 的中点,连接
的中点,连接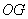
因为点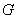 为
为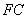 中点,所以
中点,所以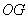 为
为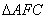 的中位线,
的中位线,
所以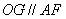 2分
2分

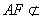 面
面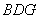 ,
,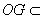 面
面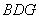 ,
,
所以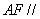 面
面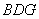 4分
4分
(2)取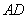 中点
中点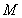 ,
,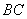 的中点
的中点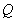 ,连接
,连接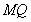 ,则
,则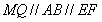 ,
,
所以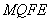 共面
共面
作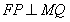 于
于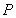 ,
,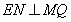 于
于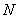 ,则
,则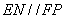 且
且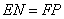
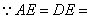
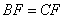 ,
,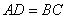
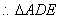 和
和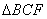 全等,
全等,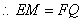
 和
和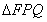 全等,
全等,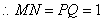

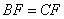 ,
,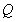 为
为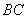 中点,
中点,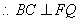
又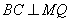 ,
,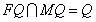 ,
,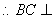 面
面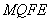
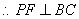 ,
,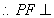 面
面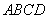 6分
6分

以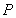 为原点,
为原点,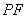 为
为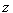 轴建立空间直角坐标系如图所示,则
轴建立空间直角坐标系如图所示,则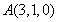 ,
,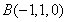 ,
,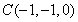 ,设
,设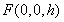 ,则
,则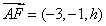 ,
,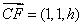
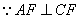 ,
,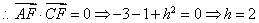
设面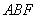 的法向量
的法向量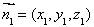
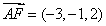 ,
,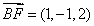
由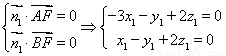 ,令
,令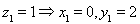
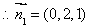 8分
8分
设面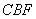 的法向量
的法向量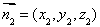
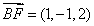 ,
,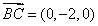
由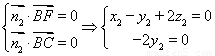 ,令
,令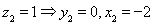
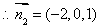 10分
10分
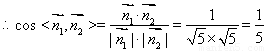
设二面角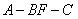 的平面角为
的平面角为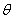 ,
,
则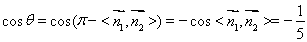 12分
12分
考点:直线与平面、平面与平面垂直,二面角的定义,空间向量的应用.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,在几何体中,四边形ABCD为平行四边形,且∠ACB=90°,平面ACE⊥平面ABCD,EF∥BC,AC=BC=2,AE=EC=
如图,在几何体中,四边形ABCD为平行四边形,且∠ACB=90°,平面ACE⊥平面ABCD,EF∥BC,AC=BC=2,AE=EC=
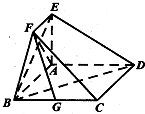 在如图所示的几何体中,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=4,AE=EF=2.
在如图所示的几何体中,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=4,AE=EF=2.