题目内容
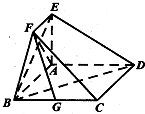 在如图所示的几何体中,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=4,AE=EF=2.
在如图所示的几何体中,四边形ABCD为矩形,EA⊥平面ABCD,EF∥AB,AB=4,AE=EF=2. (1)若G为BC的中点,求证:FG∥平面BDE;
(2)求证:AF⊥平面FBC.
分析:(1)设直线AC、BD相交于点O,连结OE、OG.矩形ABCD中,证出OG=
AB且OG∥AB,结合题意可得EF∥OG且EF=OG,得四边形EFGO是平行四边形,从而得到FG∥EO结合线面平行判定定理,即可得出FG∥平面BDE;
(2)由EA⊥平面ABCD和BC⊥AB,结合线面垂直的判定与性质证出BC⊥平面ABEF,从而AF⊥BC.直角梯形中,利用题中数据算出AF2+BF2=16=AB2,从而可得AF⊥BF,再由BF、BC是平面FBC内的相交直线,可证出AF⊥平面FBC.
| 1 |
| 2 |
(2)由EA⊥平面ABCD和BC⊥AB,结合线面垂直的判定与性质证出BC⊥平面ABEF,从而AF⊥BC.直角梯形中,利用题中数据算出AF2+BF2=16=AB2,从而可得AF⊥BF,再由BF、BC是平面FBC内的相交直线,可证出AF⊥平面FBC.
解答:解:(1)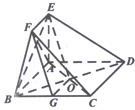 设直线AC、BD相交于点O,连结OE、OG,
设直线AC、BD相交于点O,连结OE、OG,
∵矩形ABCD中,O是AC的中点,G为BC的中点
∴OG是△ABC的中位线,可得OG=
AB且OG∥AB
又∵EF∥AB,且EF=
AB,
∴EF∥OG且EF=OG,可得四边形EFGO是平行四边形
由此可得FG∥EO
∵FG?平面BDE,OE?平面BDE,
∴FG∥平面BDE;
(2)∵EA⊥平面ABCD,BC?平面ABCD,∴EA⊥BC
又∵BC⊥AB,AB∩EA=A,∴BC⊥平面ABEF
∵AF?平面ABEF,∴AF⊥BC
∵直角梯形AEFB中,AB=4,AE=EF=2
∴AF=BF=2
,可得AF2+BF2=16=AB2,
∴△ABF是以AB为斜边的直角三角形,可得AF⊥BF
∵BF、BC是平面FBC内的相交直线
AF⊥平面FBC.
 设直线AC、BD相交于点O,连结OE、OG,
设直线AC、BD相交于点O,连结OE、OG,∵矩形ABCD中,O是AC的中点,G为BC的中点
∴OG是△ABC的中位线,可得OG=
| 1 |
| 2 |
又∵EF∥AB,且EF=
| 1 |
| 2 |
∴EF∥OG且EF=OG,可得四边形EFGO是平行四边形
由此可得FG∥EO
∵FG?平面BDE,OE?平面BDE,
∴FG∥平面BDE;
(2)∵EA⊥平面ABCD,BC?平面ABCD,∴EA⊥BC
又∵BC⊥AB,AB∩EA=A,∴BC⊥平面ABEF
∵AF?平面ABEF,∴AF⊥BC
∵直角梯形AEFB中,AB=4,AE=EF=2
∴AF=BF=2
| 2 |
∴△ABF是以AB为斜边的直角三角形,可得AF⊥BF
∵BF、BC是平面FBC内的相交直线
AF⊥平面FBC.
点评:本题给出底面为正方形、一个侧面为直角梯形的多面体,求证线面平行和线面垂直.着重考查了线面垂直的判定与性质和线面平行判定定理等知识,属于中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
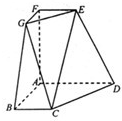 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.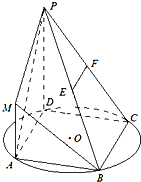 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1, 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.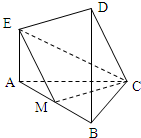 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.