Question

【题目】有下列四个命题：（1）一定存在直线，使函数的图像与函数的图像关于直线对称；（2）不等式：的解集为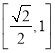；（3）已知数列的前项和为，，则数列一定是等比数列；（4）过抛物线上的任意一点的切线方程一定可以表示为.则正确命题的序号为_________________.

Answer 1

【答案】（3）（4）

【解析】

（1）中，可利用函数与关于轴对称进行判定；

（2）中，利用反三角函数的定义，直接求出符合条件的解集，即可判定；

（3）利用求得数列的通项公式，即可判定；

（4）利用直线过点，且与抛物线有且仅有一个交点，即可判定.

对于（1）中，由函数与关于轴对称，而函数的图像与函数的图象向上平移的幅度不一样，所以它们不关于轴对称，所以找不到这样的直线满足题意，所以不正确；

对于（2）中，因为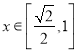时，，

所以不等式的解集为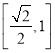是不正确的；

对于（3）中，由，当时，，满足上式，

所以数列是一个等比数列，

所以数列的前项和为，，则数列一定是等比数列是正确的；

对于（4）中，由直线过点，且与抛物线有且仅有一个交点，所以过抛物线上的任意一点的切线方程一定可以表示为是正确的.

故答案为：（3）（4）.