题目内容
如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为45°.
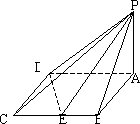
(1)求点A到平面PDE的距离;
(2)在PA上确定一点F,使BF∥平面PDE;
(3)求异面直线PC与DE所成的角(用反三角函数表示);
(4)求面PDE与面PAB所成的不大于直二面角的二面角的大小(用反三角函数表示).
答案:
解析:
解析:
|
(1)DE为正△BCD的中线,DE⊥BC,∴DE⊥AD,又PA⊥平面ABCD,DE⊥PD,∠PDA=45°,作AH⊥PD于H,则DE⊥AH,∴AH⊥平面PDE,PA=AD=2, AH= (2)F为PA的中点,可证BF∥EH,∴BF∥平面PDE. (3)延长AD到G,使DG=EC,连CG、PG,可证CG∥DE,△PCG中,CG= PC= (4)设 |

练习册系列答案
相关题目
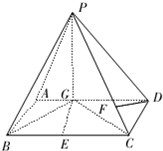 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且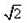 ,F是BC的中点.
,F是BC的中点.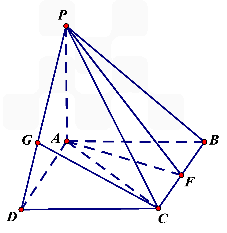
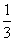 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.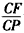 的值。
的值。 
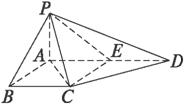
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.