题目内容
如图,圆心在原点、半径为R的圆交x轴正半轴于点A,P、Q是圆上的两个动点,它们同时从点A出发沿圆周做匀速运动.OP逆时针方向每秒转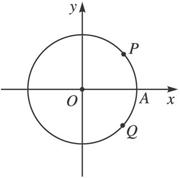
解:易知,动点P、Q由第k次相遇到第k+1次相遇所走过的弧长之和恰好等于圆的一个周长2πR,因此当他们第五次相遇时走过的弧长之和为10πR.设动点P、Q自A点出发到第五次相遇走过的时间为t秒,走过的弧长分别为l1、l2,则l1=![]() tR,l2=|-
tR,l2=|-![]() |·tR=
|·tR=![]() tR.因此l1+l2=
tR.因此l1+l2=![]() tR+
tR+![]() tR=10πR,所以t=
tR=10πR,所以t= =20(秒),l1=
=20(秒),l1=![]() πR,l2=
πR,l2=![]() πR.由此可知,OP转过的角度为
πR.由此可知,OP转过的角度为![]() π=6π+
π=6π+![]() ,所以动点P、Q第五次相遇处点M的坐标为(Rcos
,所以动点P、Q第五次相遇处点M的坐标为(Rcos![]() ,Rsin
,Rsin![]() ),即(
),即(![]() ),P、Q走过的弧长分别为
),P、Q走过的弧长分别为![]() R和
R和![]() R.
R.

练习册系列答案
相关题目
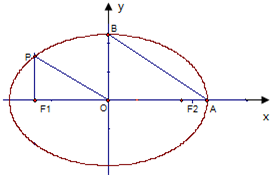 如图,从椭圆E:
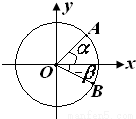
如图,从椭圆E: (2009•黄浦区一模)如图所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为α和-β.
(2009•黄浦区一模)如图所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为α和-β.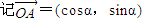 ,
,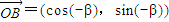 ,用两种方法计算
,用两种方法计算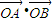 后,利用等量代换可以得到的等式是 .
后,利用等量代换可以得到的等式是 .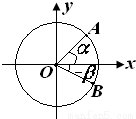
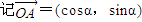 ,
,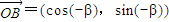 ,用两种方法计算
,用两种方法计算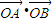 后,利用等量代换可以得到的等式是 .
后,利用等量代换可以得到的等式是 .