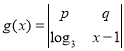题目内容
【题目】(1)集合![]() ,
,![]() 或
或![]() ,对于任意
,对于任意![]() ,定义
,定义![]() ,对任意
,对任意![]() ,定义
,定义![]() ,记
,记![]() 为集合
为集合![]() 的元素个数,求
的元素个数,求![]() 的值;
的值;
(2)在等差数列![]() 和等比数列
和等比数列![]() 中,
中,![]() ,
,![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中,若存在,求出所有的
中,若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)已知当![]() 时,有
时,有![]() ,根据此信息,若对任意
,根据此信息,若对任意![]() ,都有
,都有![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 为正偶数;(3)
为正偶数;(3)![]() ;
;
【解析】
(1)由题意得:集合![]() 表示方程
表示方程![]() 解的集合,由于
解的集合,由于![]() 或
或![]() ,即可得到集合
,即可得到集合![]() 的元素个数
的元素个数![]() ;利用倒序相加法及
;利用倒序相加法及![]() ,即可得到答案;
,即可得到答案;
(2)假设存在![]() ,对
,对![]() 分奇数和偶数两种情况进行讨论;
分奇数和偶数两种情况进行讨论;
(3)利用类比推理和分类计数原理可得![]() 的值.
的值.
(1)由题意得:集合![]() 表示方程
表示方程![]() 解的集合,
解的集合,
由于![]() 或
或![]() ,所以方程
,所以方程![]() 中有
中有![]() 个
个![]() ,
,![]() 个
个![]() ,
,
从而可得到解的情况共有![]() 个,
个,
所以![]() .
.
令![]()
![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,即
,即![]() .
.
(2)当![]() 取偶数
取偶数![]() 时,
时,![]() 中所有项都是
中所有项都是![]() 中的项.
中的项.
由题意:![]() 均在数列
均在数列![]() 中,当
中,当![]() 时,
时,
![]()
![]() ,
,
说明数列![]() 的第
的第![]() 项是数列
项是数列![]() 中的第
中的第![]() 项.
项.
当![]() 取奇数
取奇数![]() 时,因为
时,因为![]() 不是整数,所以数列
不是整数,所以数列![]() 的所有项都不在数列
的所有项都不在数列![]() 中.
中.
综上所述:![]() 为正偶数.
为正偶数.
(3)当![]() 时,有
时,有![]() ①
①
当![]() 时,
时,![]() ②
②
又对任意![]() ,都有
,都有![]() ③
③
所以![]() 即为
即为![]() 的系数,
的系数,
可取①中![]() 、②中的1;或①中
、②中的1;或①中![]() 、②中的
、②中的![]() ;或①中
;或①中![]() 、②中的
、②中的![]() ;
;
或①中的![]() 、②中的
、②中的![]() ;
;
所以![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目