题目内容
13.若函数f(x)=log2$\frac{x-a}{x+1}$的反函数的图象经过点(-2,3),则a=2.分析 由函数f(x)=log2$\frac{x-a}{x+1}$的反函数的图象经过点(-2,3),得函数f(x)=log2$\frac{x-a}{x+1}$的图象经过点(3,-2),代入计算可得结论.
解答 解:∵函数f(x)=log2$\frac{x-a}{x+1}$的反函数的图象经过点(-2,3),
∴函数f(x)=log2$\frac{x-a}{x+1}$的图象经过点(3,-2),
∴-2=log2$\frac{3-a}{3+1}$,
∴a=2,
故答案为2.
点评 本题考查了反函数,考查学生的计算能力,属于基础题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
3.某频率的分布表如下:
偏差(微米):-20~-15,-15~-10,-10~-5,-5~0,0~5,5~10,10~15,15~20.
频率分别是:0.035,0.055,0.075,0.120,0.245,0.205,0.130,0.135,则偏差小于10的累计频率是( )
偏差(微米):-20~-15,-15~-10,-10~-5,-5~0,0~5,5~10,10~15,15~20.
频率分别是:0.035,0.055,0.075,0.120,0.245,0.205,0.130,0.135,则偏差小于10的累计频率是( )
| A. | 0.265 | B. | 0.205 | C. | 0.450 | D. | 0.735 |
4.已知抛物线C:x2=12y的焦点为F,准线为l,P∈l,Q是线段PF与C的一个交点,若|PF|=3|FQ|.则|FQ|=( )
| A. | $\frac{9}{2}$ | B. | $\frac{7}{2}$ | C. | 4 | D. | 5 |
5.设α-l-β是二面角,直线a在平面α内,直线b在平面β内,且a、b与l均不垂直,则( )
| A. | a与b可能垂直,但不可能平行 | B. | a与b可能垂直也可能平行 | ||
| C. | a与b不可能垂直,但可能平行 | D. | a与b不可能垂直,也不可能平行 |
2.已知某公司现有职员120人,中级管理人员30人,高级管理人员10人,要从其中抽取32个人进行身体健康检查,如果采用分层抽样的方法,则职员中“中级管理人员“和“高级管理人员”各应该抽取的人数为( )
| A. | 8,2 | B. | 8,3 | C. | 6,3 | D. | 6,2 |
3.已知P是以F1,F2为焦点的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的一点,若PF1⊥PF2,且|PF1|=2|PF2|,则此椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{5}}{3}$ |
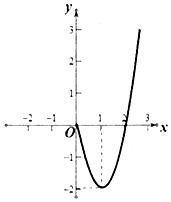 已知函数y=f(x)定义在实数集R上的奇函数,当x≥0时,函数y=f(x)的图象如图所示(抛物线的一部分).
已知函数y=f(x)定义在实数集R上的奇函数,当x≥0时,函数y=f(x)的图象如图所示(抛物线的一部分).