题目内容
已知向量 ,
, ,
, ,函数
,函数 ,
, .若对于任一实数x,f(x)与g(x)的值至少有一个为正数,则实数m的取值范围是( )
.若对于任一实数x,f(x)与g(x)的值至少有一个为正数,则实数m的取值范围是( )A.(0,2)
B.(0,8)
C.(2,8)
D.(0,4]
【答案】分析:先求出f(x)与g(x)的解析式,当m≤0时,显然不成立;当m>0时,因为f(0)=1>0,所以仅对对称轴进行讨论即可.
解答:解:由题意可得 =2mx2+2mx-8x+1=2mx2-2(4-m)x+1,
=2mx2+2mx-8x+1=2mx2-2(4-m)x+1, =mx,
=mx,
当m≤0时,显然不成立.
当m>0时,因f(0)=1>0,
当- =
= ≥0,即0<m≤4时结论显然成立.
≥0,即0<m≤4时结论显然成立.
当- =
= <0时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8.
<0时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8.
综上可得,0<m<8
故选B.
点评:本题主要考查对二次函数图象的理解,对于二次函数的图象,一定要注意其开口方向、对称轴和判别式,体现了分类讨论的数学思想,属于中档题.
解答:解:由题意可得
 =2mx2+2mx-8x+1=2mx2-2(4-m)x+1,
=2mx2+2mx-8x+1=2mx2-2(4-m)x+1, =mx,
=mx,当m≤0时,显然不成立.
当m>0时,因f(0)=1>0,
当-
 =
= ≥0,即0<m≤4时结论显然成立.
≥0,即0<m≤4时结论显然成立.当-
 =
= <0时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8.
<0时,只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8.综上可得,0<m<8
故选B.
点评:本题主要考查对二次函数图象的理解,对于二次函数的图象,一定要注意其开口方向、对称轴和判别式,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目




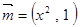 ,
, ,其中
,其中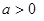 .函数
.函数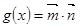 在区间
在区间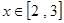 上有最大值为4,设
上有最大值为4,设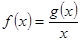 .
.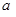 的值;
的值;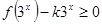 在
在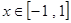 上恒成立,求实数
上恒成立,求实数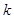 的取值范围.
的取值范围. ,
, ,设函数
,设函数 .
. 的最小正周期与单调递增区间;
的最小正周期与单调递增区间;  中,
中, 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,若
的对边,若 △
△ ,求
,求 ,
, ,设函数
,设函数 .
. 的最小正周期及在
的最小正周期及在 上的最大值;
上的最大值; 的角A、B、C所对的边分别为a、b、c,A、B为锐角,
的角A、B、C所对的边分别为a、b、c,A、B为锐角, ,
, ,又
,又 ,求a、b、c的值.
,求a、b、c的值.