题目内容
 如图示,在△ABC中,若A,B两点坐标分别为(2,0),(-3,4)点C在AB上,且OC平分∠BOA.
如图示,在△ABC中,若A,B两点坐标分别为(2,0),(-3,4)点C在AB上,且OC平分∠BOA.
(1)求∠AOB的余弦值;
(2)求点C的坐标.
解:(1)由题意可得,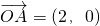 ,
,
∴ =
= =
=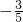
(2)设点C(x,y),由OC平分∠BOA可得cos∠AOC=cos∠BOC
∵ ,
,
∴ =
=
∴ ,
,
∴y=2x①
又点C在AB即
 共线,
共线,
∴4x+5y-8=0②
由①②解得 ,
,
∴点C的坐标为
分析:(1)由题意可得 ,把已知代入可求
,把已知代入可求
(2)设点C(x,y),由OC平分∠BOA可得cos∠AOC=cos∠BOC即 =
= ;再由点C在AB即
;再由点C在AB即
 共线,建立关于x,y的关系,可求
共线,建立关于x,y的关系,可求
点评:本题注意考查了向量的夹角公式的坐标表示的应用,向量共线的坐标表示在三角形中的应用,解题的关键是借助于已知图象中的条件,灵活的应用向量的基本知识.
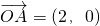 ,
,
∴
 =
= =
=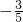
(2)设点C(x,y),由OC平分∠BOA可得cos∠AOC=cos∠BOC
∵
 ,
,
∴
 =
=
∴
 ,
,∴y=2x①
又点C在AB即

 共线,
共线,
∴4x+5y-8=0②
由①②解得
 ,
,∴点C的坐标为

分析:(1)由题意可得
 ,把已知代入可求
,把已知代入可求(2)设点C(x,y),由OC平分∠BOA可得cos∠AOC=cos∠BOC即
 =
= ;再由点C在AB即
;再由点C在AB即
 共线,建立关于x,y的关系,可求
共线,建立关于x,y的关系,可求点评:本题注意考查了向量的夹角公式的坐标表示的应用,向量共线的坐标表示在三角形中的应用,解题的关键是借助于已知图象中的条件,灵活的应用向量的基本知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图示,在△ABC中,若A,B两点坐标分别为(2,0),(-3,4)点C在AB上,且OC平分∠BOA.
如图示,在△ABC中,若A,B两点坐标分别为(2,0),(-3,4)点C在AB上,且OC平分∠BOA. ,BC
= 6.
,BC
= 6.

