Question

已知直线C₁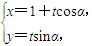： ，(t为参数)，圆C₂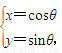： (θ为参数)．

（I）当α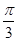＝时，求C₁与C₂的交点的直角坐标；

（II）过坐标原点O作C₁的垂线，垂足为A，P为OA的中点．当α变化时，求P点轨迹的参数方程，并指出它是什么曲线．

 

Answer 1

【答案】

（I）C₁与C₂的交点为(1,0)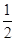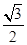，(，－)．（II）P点轨迹是圆心为(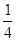，0)，半径为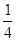的圆．

【解析】本试题主要是考查了参数方程与极坐标方程之间的转换以及直线与圆的位置关系的运用。利用参数方程消去参数的思想求解轨迹方程的综合运用。

（1）当α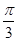＝时，C₁的普通方程为y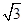＝(x－1)，C₂的普通方程为x²＋y²＝1.

联立方程组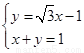，解得C₁与C₂的交点为(1,0)，(，－)

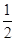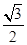（II）由C₁的普通方程为xsinα－ycosα－sinα＝0.

A点坐标为(sin²α，－cosαsinα)，故当α变化时，P点轨迹的参数方程为

 ，消去参数求解得到轨迹方程

解：（I）当α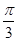＝时，C₁的普通方程为y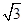＝(x－1)，C₂的普通方程为x²＋y²＝1.

联立方程组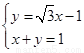，解得C₁与C₂的交点为(1,0)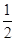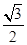，(，－)．…（5分）

（II）C₁的普通方程为xsinα－ycosα－sinα＝0.

A点坐标为(sin²α，－cosαsinα)，

故当α变化时，P点轨迹的参数方程为

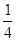 ，(α为参数)． P点轨迹的普通方程为(x－)²＋y²＝.

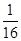故P点轨迹是圆心为(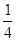，0)，半径为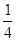的圆．