题目内容
已知函数 .
.
(1)求函数f(x)在(0,2)上的最小值;
(2)设g(x)=-x2+2mx-4,若对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,求实数m的取值范围.
解:(1)求导函数,可得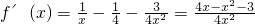
∵0<x<2,令f′(x)>0,可得1<x<2;令f′(x)>0,可得0<x<1
∴函数f(x)在(0,2)上的单调递增区间是(1,2),单调递减区间是(0,1)
∴函数f(x)在x=1处,取得极小值,且为最小值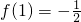
(2)由(1)知,f(x)min=
对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,等价于-x2+2mx-4 ,x,∈[1,2]恒成立.
,x,∈[1,2]恒成立.
∴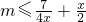 ,x,∈[1,2]恒成立.
,x,∈[1,2]恒成立.
∵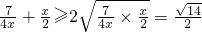 ,当且仅当
,当且仅当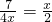 ,即
,即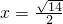 时取等号
时取等号
∴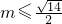
∴实数m的取值范围为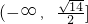
分析:(1)求导函数,确定函数f(x)在(0,2)上的单调性,从而可得函数f(x)的极小值,即可求出最小值;
(2)由(1)知,f(x)min= 对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,等价于-x2+2mx-4
对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,等价于-x2+2mx-4 ,x,∈[1,2]恒成立,利用分离参数法及基本不等式,即可求得实数m的取值范围.
,x,∈[1,2]恒成立,利用分离参数法及基本不等式,即可求得实数m的取值范围.
点评:本题考查导数知识的运用,考查恒成立问题,考查分离参数法的运用,解题的关键是利用导数确定函数的单调性与最值.
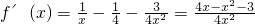
∵0<x<2,令f′(x)>0,可得1<x<2;令f′(x)>0,可得0<x<1
∴函数f(x)在(0,2)上的单调递增区间是(1,2),单调递减区间是(0,1)
∴函数f(x)在x=1处,取得极小值,且为最小值
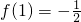
(2)由(1)知,f(x)min=

对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,等价于-x2+2mx-4
 ,x,∈[1,2]恒成立.
,x,∈[1,2]恒成立.∴
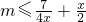 ,x,∈[1,2]恒成立.
,x,∈[1,2]恒成立.∵
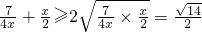 ,当且仅当
,当且仅当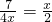 ,即
,即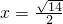 时取等号
时取等号∴
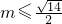
∴实数m的取值范围为
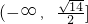
分析:(1)求导函数,确定函数f(x)在(0,2)上的单调性,从而可得函数f(x)的极小值,即可求出最小值;
(2)由(1)知,f(x)min=
 对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,等价于-x2+2mx-4
对任意x1∈(0,2),x2∈[1,2],不等式f(x1)≥g(x2)恒成立,等价于-x2+2mx-4 ,x,∈[1,2]恒成立,利用分离参数法及基本不等式,即可求得实数m的取值范围.
,x,∈[1,2]恒成立,利用分离参数法及基本不等式,即可求得实数m的取值范围.点评:本题考查导数知识的运用,考查恒成立问题,考查分离参数法的运用,解题的关键是利用导数确定函数的单调性与最值.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.