题目内容
设函数![]() ,其中
,其中![]() 为常数。
为常数。
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若函数![]() 有极值点,求
有极值点,求![]() 的取值范围及
的取值范围及![]() 的极值点。
的极值点。
(Ⅰ)当![]() 时,
时, ![]() ,函数
,函数![]() 在定义域
在定义域![]() 上单调递增.
上单调递增.
(Ⅱ)当且仅当![]() 时
时![]() 有极值点;
有极值点;
当![]() 时,
时,![]() 有惟一最小值点
有惟一最小值点![]() ;
;
当![]() 时,
时,![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]()
解析:
(Ⅰ)由题意知,![]() 的定义域为
的定义域为![]() , ……… 1分
, ……… 1分
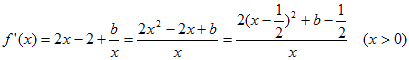 ……… 2分
……… 2分
∴当![]() 时,
时, ![]() ,函数
,函数![]() 在定义域
在定义域![]() 上单调递增. ………………3分
上单调递增. ………………3分
(Ⅱ)①由(Ⅰ)得,当![]() 时,函数
时,函数![]() 无极值点.………… 4分
无极值点.………… 4分
②![]() 时,
时,![]() 有两个相同的解
有两个相同的解![]() ,
,
但当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 时,函数
时,函数![]() 在
在![]() 上无极值点. ………………5分
上无极值点. ………………5分
③当![]() 时,
时,![]() 有两个不同解,
有两个不同解,
![]()
![]()
![]() 时,
时,![]() ,
,
而![]() ,
,
此时 ![]() ,
,![]() 随
随![]() 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 减 | 极小值 | 增 |
由此表可知:当![]() 时,
时,![]() 有惟一极小值点
有惟一极小值点![]() ,… 8分
,… 8分
ii) 当![]() 时,0<
时,0<![]() <1
<1
此时,![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 增 | 极大值 | 减 | 极小值 | 增 |
由此表可知:![]() 时,
时,![]() 有一个极大值
有一个极大值![]() 和一个极小值点
和一个极小值点![]() ; ………………………………11分
; ………………………………11分
综上所述:
当且仅当![]() 时
时![]() 有极值点;
有极值点;
当![]() 时,
时,![]() 有惟一最小值点
有惟一最小值点![]() ;
;
当![]() 时,
时,![]() 有一个极大值点
有一个极大值点![]() 和一个极小值点
和一个极小值点![]() ………12分
………12分

练习册系列答案
相关题目
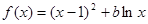 ,其中
,其中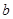 为常数。
为常数。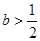 时,判断函数
时,判断函数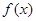 在定义域上的单调性;
在定义域上的单调性;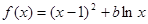 ,其中
,其中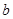 为常数。
为常数。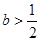 时,判断函数
时,判断函数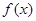 在定义域上的单调性;
在定义域上的单调性;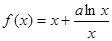 ,其中
,其中 为常数.
为常数. ,
, 的图象恒过定点;
的图象恒过定点;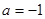 时,判断函数
时,判断函数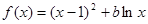 ,其中
,其中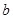 为常数.
为常数. 时,判断函数
时,判断函数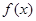 在定义域上的单调性;
在定义域上的单调性;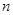 ,不等式
,不等式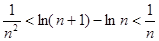 都成立.
都成立.