Question

【题目】已知函数

（1）若对任意的 恒成立，求实数的最小值.

（2）若 且关于的方程 在 上恰有两个不相等的实数根，求实数 的取值范围；

（3）设各项为正的数列 满足： 求证：

Answer 1

【答案】（1） ； （2） ； （3）

【解析】试题分析：（I）依题意，对任意的， 恒成立，即在恒成立，则，而，所以在是减函数， 最大值为1，所以， ，实数的最小值。

（II）因为，且在上恰有两个不相等的实数根，即在上恰有两个不相等的实数根，

设，则

列表：

X	(0, )		(,2)	2	(2,4)
	+	0	-	0	+
	增函数	极大值	减函数	极小值	增函数

所以极大值， 极大值， ， ，因为方程在上恰有两个不相等的实数根．

则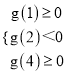，解得．

（III）设， ，则，∴在为减函数，且，故当时有，∵，假设（），则，故（），从而，∴，即，∴