题目内容
已知双曲线
的左、右焦点分别为F1，F2，其一条渐近线方程为y=x，点
在该双曲线上，则
=________．
0
分析：由题设知b=
，再根据点在该双曲线上知y02=1．由此能求出．
解答：∵双曲线的渐近线方程为y=
，
∴
．
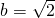把点代入双曲线，得
，解得y02=1．
∴P（
），F1（-2，0），F2（2，0），=（-2-
，0-1）
=0，
或P（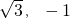
），F1（-2，0），F2（2，0），=（-2-，0+1）
=0．
故答案为0．
点评：本题考查双曲线的简单性质，解题时要认真审题，仔细解答．
分析：由题设知b=
，再根据点在该双曲线上知y02=1．由此能求出．解答：∵双曲线
的渐近线方程为y=，∴
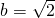．把点
代入双曲线，得，解得y02=1．∴P（
），F1（-2，0），F2（2，0），=（-2-，0-1）=0，或P（
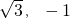），F1（-2，0），F2（2，0），=（-2-，0+1）=0．故答案为0．
点评：本题考查双曲线的简单性质，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
的方程为 
，双曲线
的左、右焦
与双曲线C2恒有两个不同的交点A和B，求
的范围。
的左、右焦 点分别为F1、F2，P为C的右支上一点，且
的面积等于 ．
的左、右焦 点分别为F1、F2，P为C的右支上一点，且
的面积等于 ．